Edexcel A Level (IAL) Physics-1.29 Force–Extension Graphs- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -1.29 Force–Extension Graphs- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -1.29 Force–Extension Graphs- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
- 1.29 a) be able to draw and interpret force-extension and force-compression graphs
b) understand the terms limit of proportionality, elastic limit, yield point, elastic deformation and plastic deformation and be able to apply them to these graphs
Force–Extension and Force–Compression Graphs, and Key Elasticity Terms
This section explains how to interpret force–extension and force–compression graphs, and defines the key terms used in material deformation.
Force–Extension Graphs
These graphs show how the extension \( \Delta x \) of an object (typically a spring or wire) changes as the applied force \( F \) increases.
![]()
- Horizontal axis: Extension (m)
- Vertical axis: Force (N)
- For many materials, the graph begins as a straight line → obeys Hooke’s Law.
- The slope of the linear region = stiffness \( k \).
Key features:
- Straight-line region → proportional behaviour.
- Curve begins to bend → material approaching elastic limit.
- Beyond a certain point, extension increases rapidly for small increases in force.
- The material eventually reaches a breaking point.
Force–Compression Graphs
These are similar to force–extension graphs but apply to objects being squashed rather than stretched.

- Many materials behave similarly in compression and extension.
- Foams and rubber show different behaviour with hysteresis (energy loss).
- Spring compression graphs should follow Hooke’s Law if deformation is elastic.
Key Terms in Elasticity
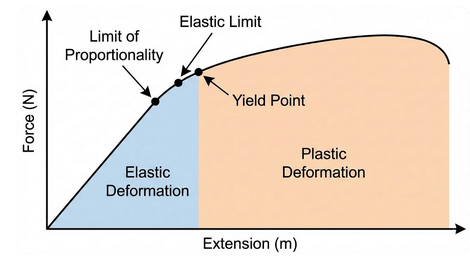
Limit of Proportionality
- The point where the graph stops being a straight line. Hooke’s Law (\( F = k\Delta x \)) holds only up to this point.
Elastic Limit
- The maximum force after which the material will not return to its original length when the force is removed. Elastic behaviour ends here.
Yield Point
- The point at which a small increase in force causes a large increase in extension. The material begins to deform plastically and permanently.
Elastic Deformation
- Material returns to its original shape when the force is removed. Work done is stored as elastic potential energy.
Plastic Deformation
- Permanent deformation — the material does not return to its original length when the force is removed.
How to Interpret the Graph
- From the origin to limit of proportionality → straight line.
- Between limit of proportionality and elastic limit → non-linear elastic region.
- Between elastic limit and yield point → beginning of plastic deformation.
- Beyond yield point → significant plastic deformation.
- Very end of the graph → breaking stress / fracture.
Energy Stored in a Material (Optional: exams sometimes ask)
Area under the force–extension graph = work done.
![]()
Up to elastic limit:
\( E = \dfrac{1}{2}F\Delta x = \dfrac{1}{2}k(\Delta x)^2 \)
Example (Easy)
A material obeys Hooke’s Law up to a force of \( 6\, \mathrm{N} \). What does this mean?
▶️ Answer / Explanation
It means the force–extension graph is a straight line up to \( 6\, \mathrm{N} \), and:
\( F = k\Delta x \) is valid.
This point is the limit of proportionality.
Example (Medium)
A wire returns to its original length after a load is removed. What type of deformation is this?
▶️ Answer / Explanation
Elastic deformation.
The material has not crossed the elastic limit.
Example (Hard)
The force–extension graph of a material curves after a force of \( 10\, \mathrm{N} \). It reaches the elastic limit at \( 15\, \mathrm{N} \). Explain what happens between 10 N and 15 N.
▶️ Answer / Explanation
At \( 10\, \mathrm{N} \), the graph stops being proportional → reached the limit of proportionality.
Between \( 10\, \mathrm{N} \) and \( 15\, \mathrm{N} \):
- The material is still deforming elastically but not proportionally.
- Hooke’s Law is no longer valid.
- Once \( 15\, \mathrm{N} \) is reached → elastic limit → further deformation becomes plastic.
