Edexcel A Level (IAL) Physics-1.30 Stress–Strain Graphs- Study Notes- New Syllabus

Tensile and Compressive Stress–Strain Graphs and Breaking Stress

Stress–strain graphs show how materials deform under tensile (stretching) or compressive (squashing) forces. They reveal important material properties such as elasticity, stiffness, and breaking stress.

Stress–Strain Graph Overview

Stress is plotted on the vertical axis, strain on the horizontal axis:

• Vertical axis: Stress (Pa)
• Horizontal axis: Strain (dimensionless)

A typical tensile stress–strain graph includes several important regions:

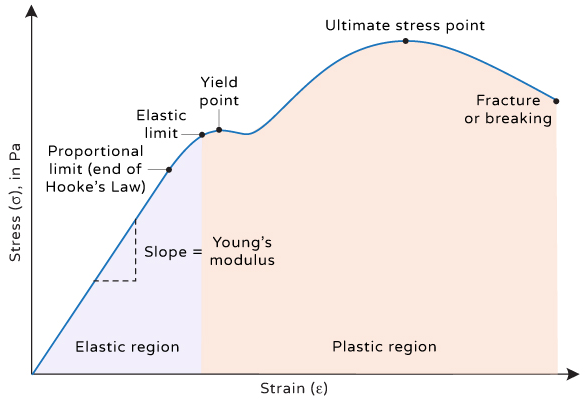
• Linear (elastic) region: Stress is proportional to strain. Young modulus is constant.
• Elastic limit: Last point where the material returns fully to original length.
• Yield point: Material begins to deform plastically.
• Plastic region: Permanent deformation occurs.
• Ultimate tensile stress (UTS): Maximum stress the material can withstand.
• Breaking point: Material fractures.

Tensile Stress–Strain Graph (Stretching)

• Starts at origin (no stress, no strain).
• Straight-line region indicates Hooke’s Law.
• After limit of proportionality, curve bends → non-linear elastic deformation.
• Beyond elastic limit → plastic deformation begins.
• Near the end → necking occurs (localised reduction in cross-section).

Important: Tensile graphs are the most commonly used in exams.

 Compressive Stress–Strain Graph (Squashing)

• Shape depends on the material.
• Brittle materials (e.g., concrete, stone) break suddenly with little plastic region.
• Ductile materials (e.g., metals) compress and deform before failure.
• Foams/rubbers show a long flat region (cell collapse) before rising steeply.

Breaking Stress

Breaking stress is the stress at which a material finally fractures.

$\text{Breaking stress} = \frac{\text{Breaking force}}{A} $

• Breaking stress is always less than the ultimate tensile stress.
• At breaking stress, internal cracks propagate rapidly.
• The material cannot withstand any further increase in stress.

 Comparing Materials

• Brittle materials (glass, ceramics):
  • Almost no plastic region.
  • Break suddenly at low strains.
  • Steep linear region, then immediate fracture.
• Ductile materials (copper, mild steel):
  • Large plastic region.
  • Undergo significant deformation before breaking.
• Polymeric materials (rubber, plastics):
  • Non-linear behaviour.
  • Large strain before breaking.

How to Interpret a Stress–Strain Graph (Exam Skills)

• Gradient of linear region = Young modulus.
• Area under graph up to elastic limit = elastic energy stored.
• Area under full graph = work done until fracture.
• Point where line stops being straight = limit of proportionality.
• Point where material stops returning to original shape = elastic limit.
• Sudden drop or plateau = yield point.
• Highest point = ultimate tensile stress.
• Final point = breaking point.