Edexcel A Level (IAL) Physics-1.31 Core Practical 3: Investigating Young Modulus- Study Notes- New Syllabus

CORE PRACTICAL 3: Determine the Young Modulus of a Material

This practical measures how much a material (usually a wire) extends when forces are applied, and uses stress–strain relationships to calculate the Young modulus.

Aim

To determine the Young modulus \( E \) of a material using the relationship:

$ E = \frac{\text{stress}}{\text{strain}} = \frac{F L_0}{A \Delta L} $

Apparatus

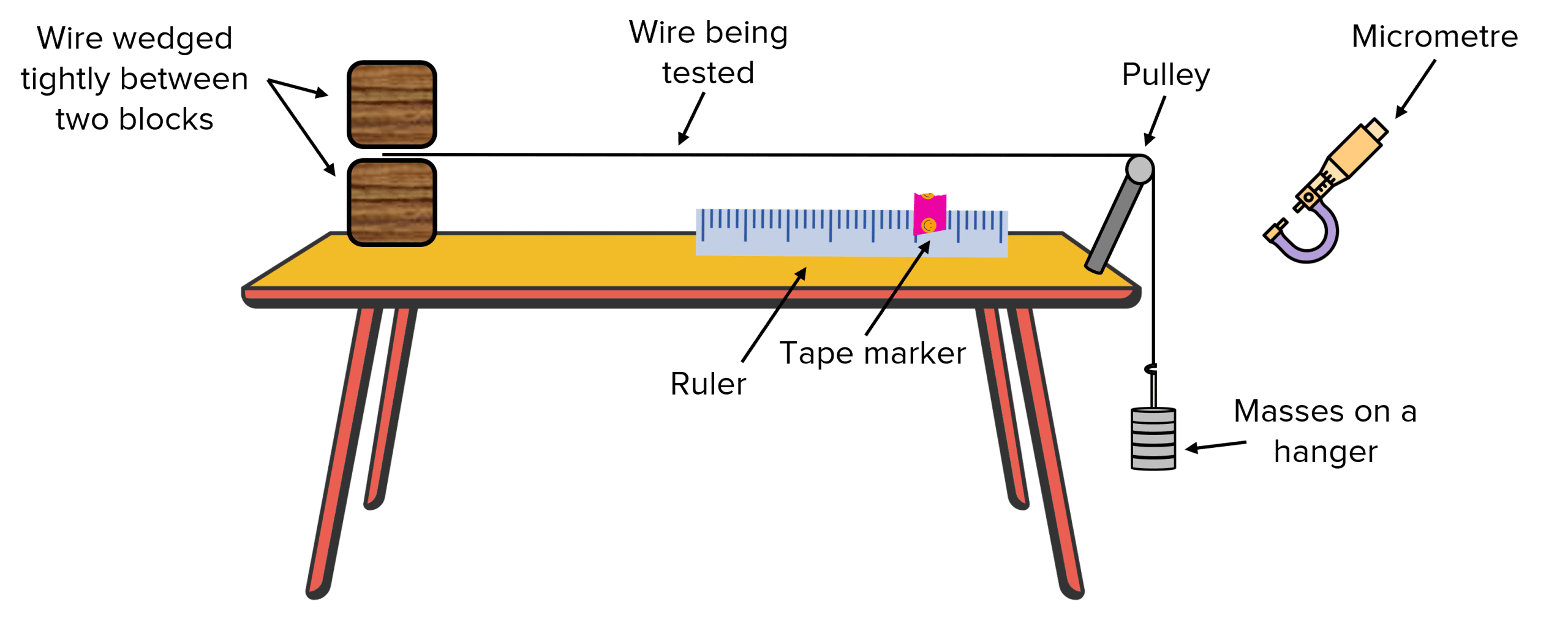
• Long test wire (e.g., nichrome)
• Micrometer screw gauge (to measure wire diameter)
• Metre ruler or measuring scale
• Clamps and stand
• Pointer attached to the wire
• Masses and mass hanger (to apply known force)
• Reference wire (to eliminate support movement)
• Vernier scale / travelling microscope (for precision)

Theory

The wire obeys:

$ \text{stress} = \frac{F}{A}, \quad \text{strain} = \frac{\Delta L}{L_0} $

So the Young modulus is:

$ E = \frac{F L_0}{A \Delta L} $

• \( F = mg \) is the applied force
• \( L_0 \) = original length of wire
• \( \Delta L \) = extension
• \( A = \pi r^2 \) = cross-sectional area

Procedure

1. Measure diameter of wire at several points using a micrometer. Take an average radius \( r \).
2. Secure the wire firmly at the top clamp. Attach a pointer at the bottom near the scale.
3. Measure the initial length \( L_0 \) of the wire from the clamp to the pointer.
4. Set up a second reference wire alongside to compensate for stand movement.
5. Hang a mass hanger on the test wire and add masses gently.
6. Record extension \( \Delta L \) for each added mass using the pointer scale.
7. Repeat readings at least three times for accuracy.
8. Plot a graph of F (y-axis) against extension ΔL (x-axis).

Data Processing

The graph should be linear in the elastic region.

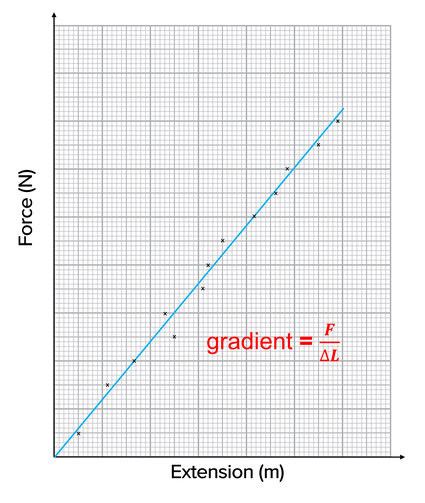
• The gradient gives stiffness \( k \):
  

  \( k = \frac{F}{\Delta L} \)

• The Young modulus can be calculated using:
  

  $ E = \frac{F L_0}{A \Delta L} $

Assumptions

• The wire obeys Hooke’s Law (within elastic limit).
• The wire is of uniform diameter.
• Temperature remains constant.
• No slipping occurs at the clamp.
• Extensions are small compared to original length.

Sources of Error

• Parallax error in reading pointer scale.
• Wire not perfectly vertical.
• Diameter of wire varies along its length.
• Wire may have initial kinks.
• Stand may move slightly (corrected using reference wire).
• Temperature changes can affect elasticity.

How to Improve Accuracy

• Use a travelling microscope to measure extension precisely.
• Use a long wire to reduce percentage errors in extension.
• Repeat diameter measurements in multiple orientations.
• Use small mass increments to avoid overshooting elastic limit.
• Plot a best-fit line on the F–ΔL graph.