Edexcel A Level (IAL) Physics-1.32 Elastic Strain Energy- Study Notes- New Syllabus

Elastic Strain Energy \( \Delta E_{\text{el}} = \tfrac{1}{2}F\,\Delta x \) and Area Under Force–Extension Graph

Elastic strain energy is the work done on a material to deform it elastically (i.e., it returns to its original shape when the force is removed).

Elastic Strain Energy Formula

For materials obeying Hooke’s Law:

$ \Delta E_{\text{el}} = \frac{1}{2} F\,\Delta x $

• \( \Delta E_{\text{el}} \) = elastic strain energy (J)
• \( F \) = applied force (N)
• \( \Delta x \) = extension (m)

This equation is valid only in the linear region where Hooke’s Law holds.

Energy from Spring Constant

If the spring constant \( k \) is known:

$ \Delta E_{\text{el}} = \frac{1}{2}k(\Delta x)^2 $

• More useful when a force-extension graph is not provided.

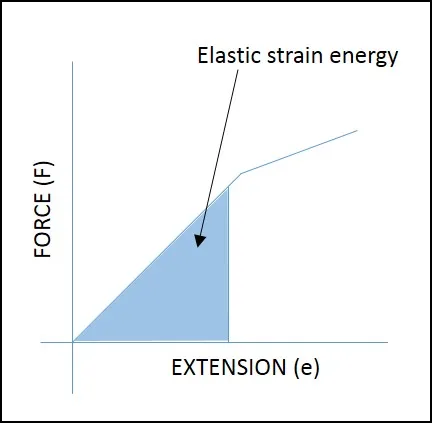
 Energy from the Area Under the Force–Extension Graph

The work done in stretching a material is:

$ \Delta E_{\text{el}} = \text{Area under the } F\text{–}x \text{ graph} $

• This works for linear and non-linear materials.
• Linear graph → area is a triangle → use \( \frac{1}{2}F\Delta x \).
• Non-linear graph → area must be estimated (trapeziums, counting squares, integration).

Linear (Hookean) Materials

• Graph is a straight line.
• Energy stored is triangular area under the line.
• Accurate and simple to calculate.

$ \Delta E_{\text{el}} = \frac{1}{2}F\Delta x $

Non-Linear Materials (Rubber, Polymers, Plastics)

• Curve is not straight → no simple formula.
• Estimate area using:
  • small trapeziums beneath the curve
  • counting squares on graph paper
  • digital integration (A-level: trapezium rule)
• The area still equals the energy stored.

 Important Notes

• Elastic strain energy is only recoverable if deformation is elastic.
• In the plastic region, work done is not fully recovered → some becomes internal energy.
• Energy stored in real materials often shows hysteresis (energy loss during unloading).