Edexcel A Level (IAL) Physics-1.4 – 1.6 Scalars & Vectors- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -1.4 – 1.6 Scalars & Vectors- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -1.4 – 1.6 Scalars & Vectors- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
- 1.4 understand scalar and vector quantities and know examples of each type of quantity and recognise vector notation
- 1.5 be able to resolve a vector into two components at right angles to each other by drawing and by calculation
- 1.6 be able to find the resultant of two coplanar vectors at any angle to each other by drawing, and at right angles to each other by calculation
Scalar and Vector Quantities
Scalar and vector quantities describe physical measurements, but they differ in whether they include direction.
![]()
1. Scalars
Definition: A scalar quantity has magnitude only and no direction.
- Fully described by a single number + unit.
- Direction is not required.
Common Scalar Quantities:
- Mass (kg)
- Temperature (°C, K)
- Speed (m s⁻¹)
- Distance (m)
- Time (s)
- Energy (J)
- Power (W)
- Density (kg m⁻³)
2. Vectors
Definition: A vector quantity has both magnitude and direction.
- Direction must be specified to fully describe the quantity.
- Vectors can be added, subtracted, and resolved into components.
Common Vector Quantities:
- Velocity (m s⁻¹)
- Displacement (m)
- Acceleration (m s⁻²)
- Force (N)
- Momentum (kg m s⁻¹)
- Weight (N)
3. Recognising Vector Notation
Vectors may be written in various formats:
![]()
- Bold letters: \( \mathrm{\mathbf{v},\ \mathbf{F}} \)
- Arrow notation: \( \mathrm{\vec{v},\ \vec{F}} \)
- Component form: \( \mathrm{ \vec{v} = (v_x,\ v_y,\ v_z) } \)
- Unit vector form: \( \mathrm{\vec{v} = v_x\hat{i} + v_y\hat{j} + v_z\hat{k}} \)
Magnitude of a vector:
\( \mathrm{|\vec{v}| = \sqrt{v_x^2 + v_y^2 + v_z^2}} \)
Direction of a vector:
- Can be stated as an angle (e.g., 30° north of east).
- Or by a unit vector \( \mathrm{\hat{v}} \).
Example (Easy)
State whether each of the following is a scalar or vector: (a) Distance (b) Velocity (c) Mass (d) Force
▶️ Answer / Explanation
(a) Distance → scalar
(b) Velocity → vector
(c) Mass → scalar
(d) Force → vector
Example (Medium)
A vector \( \mathrm{\vec{v}} \) has components \( \mathrm{(3,\ 4)} \). Find its magnitude.
▶️ Answer / Explanation
Magnitude:
\( \mathrm{|\vec{v}| = \sqrt{3^2 + 4^2}} \)
\( \mathrm{|\vec{v}| = 5} \)
Example (Hard)
A force vector is given by \( \mathrm{\vec{F} = (6,\ -8)} \). Find its magnitude and the direction it makes with the positive x–axis.
▶️ Answer / Explanation
Magnitude:
\( \mathrm{|\vec{F}| = \sqrt{6^2 + (-8)^2}} \)
\( \mathrm{|\vec{F}| = 10\ N} \)
Direction:
\( \mathrm{\theta = \tan^{-1}\left(\dfrac{-8}{6}\right)} \)
The angle is negative → direction is below the x–axis.
Resolving Vectors Into Perpendicular Components
A vector can be split (resolved) into two perpendicular components, usually along the horizontal (x) and vertical (y) directions. This is fundamental in mechanics because motion and forces often act in different dimensions independently.
1. Meaning of Resolving a Vector
To resolve a vector means to break it into two perpendicular parts that together produce the original vector.
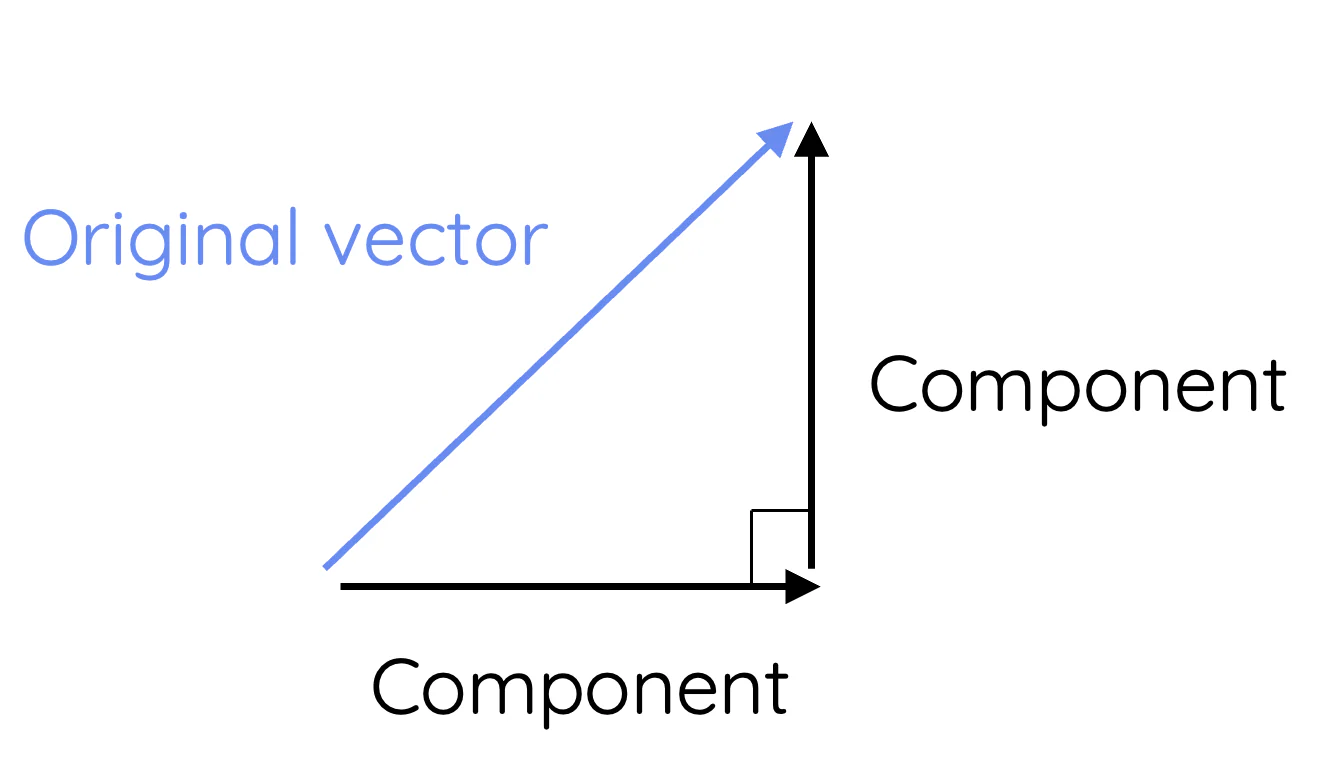
- Typically resolved into horizontal and vertical components.
- The components are at 90° to each other.
- Only valid for straight-line vector addition.
2. Vector Resolution by Drawing (Graphical Method)

Steps:
- Draw the vector to scale with correct direction.
- From the tail of the vector, draw perpendicular lines to form a right-angled triangle.
- The sides of the triangle represent the components.
- Measure the lengths using the scale to obtain component magnitudes.
Key idea: The original vector is the diagonal of the right-angled triangle formed by its components.
3. Vector Resolution by Calculation (Analytical Method)
Given a vector of magnitude \( \mathrm{F} \) at an angle \( \mathrm{\theta} \) above the horizontal:
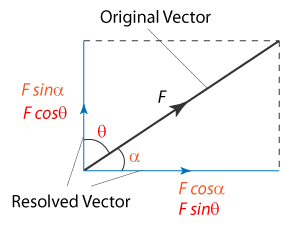
- Horizontal component: \( \mathrm{F_x = F \cos\theta} \)
- Vertical component: \( \mathrm{F_y = F \sin\theta} \)
Reversing the process (finding magnitude and direction):
- Magnitude: \( \mathrm{F = \sqrt{F_x^2 + F_y^2}} \)
- Direction: \( \mathrm{\theta = \tan^{-1}\left(\dfrac{F_y}{F_x}\right)} \)
Why This Works
- Horizontal and vertical components act independently.
- Trigonometry applies because the components form a right-angled triangle.
- Useful for analyzing motion, forces, and equilibrium.
Example (Easy)
A force of magnitude \( \mathrm{10\ N} \) acts at an angle of \( \mathrm{30^\circ} \) above the horizontal. Find its horizontal component.
▶️ Answer / Explanation
Use: \( \mathrm{F_x = F\cos\theta} \)
\( \mathrm{F_x = 10\cos30^\circ = 10\left(\dfrac{\sqrt{3}}{2}\right)} \)
\( \mathrm{F_x = 5\sqrt{3}\ N} \)
Example (Medium)
A vector of magnitude \( \mathrm{25\ m\,s^{-1}} \) makes an angle of \( \mathrm{53^\circ} \) with the horizontal. Find the horizontal and vertical components.
▶️ Answer / Explanation
Horizontal:
\( \mathrm{v_x = 25\cos53^\circ = 25(0.6) = 15\ m\,s^{-1}} \)
Vertical:
\( \mathrm{v_y = 25\sin53^\circ = 25(0.8) = 20\ m\,s^{-1}} \)
Example (Hard)
A displacement vector has components \( \mathrm{(12\ m,\ -5\ m)} \). Find the magnitude of the displacement and the direction relative to the positive x–axis.
▶️ Answer / Explanation
Magnitude:
\( \mathrm{d = \sqrt{12^2 + (-5)^2}} \)
\( \mathrm{d = 13\ m} \)
Direction:
\( \mathrm{\theta = \tan^{-1}\left(\dfrac{-5}{12}\right)} \)
The angle is negative → direction is 5 m below the horizontal.
Resultant of Two Coplanar Vectors
Two vectors are coplanar when they lie in the same plane. The resultant is the single vector that has the same effect as the two vectors combined.
1. Finding the Resultant by Drawing (Any Angle)
This is a graphical method used when vectors act at any angle to each other.
Steps (Parallelogram or Triangle Method):
![]()
![]()
- Draw the first vector to scale and in the correct direction.
- From the head (arrow) of the first vector, draw the second vector to scale.
- Join the tail of the first vector to the head of the second vector.
- This line is the resultant vector.
- Measure its length and direction using the chosen scale.
Key Idea: The resultant is the diagonal of the parallelogram or the third side of a triangle.
2. Finding the Resultant by Calculation (Vectors at 90°)
When two vectors act at right angles, trigonometry can be used. Let the two perpendicular vectors be:

- Horizontal component: A
- Vertical component: B
Magnitude of resultant:
\( \mathrm{R = \sqrt{A^2 + B^2}} \)
Direction of resultant:
\( \mathrm{\theta = \tan^{-1}\left(\dfrac{B}{A}\right)} \)
- \( \mathrm{\theta} \) measured from horizontal.
- Handles both positive and negative components.
- This method works only when vectors are perpendicular.
3. Why These Methods Work
- Vectors follow geometric addition.
- Right-angled cases use Pythagoras and trigonometry.
- Any-angle cases require drawing because exact trig becomes complicated.
- Resultants help simplify force and motion analysis.
Example (Easy)
Two perpendicular vectors act on a point: \( \mathrm{A = 6\ N} \) horizontally and \( \mathrm{B = 8\ N} \) vertically. Find the resultant.
▶️ Answer / Explanation
Magnitude:
\( \mathrm{R = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = 10\ N} \)
Direction:
\( \mathrm{\theta = \tan^{-1}\left(\dfrac{8}{6}\right)} \)
This angle is above the horizontal.
Example (Medium)
Two vectors \( \mathrm{12\ N} \) and \( \mathrm{9\ N} \) act at right angles. Find the magnitude and direction of the resultant.
▶️ Answer / Explanation
Magnitude:
\( \mathrm{R = \sqrt{12^2 + 9^2} = \sqrt{144 + 81} = 15\ N} \)
Direction:
\( \mathrm{\theta = \tan^{-1}\left(\dfrac{9}{12}\right)} \)
Angle is above the 12 N vector.
Example (Hard)
Two forces act on a point: – \( \mathrm{F_1 = 20\ N} \) – \( \mathrm{F_2 = 15\ N} \) The angle between them is \( \mathrm{60^\circ} \). Find the magnitude of the resultant using the law of cosines (analytical method for any angle).
▶️ Answer / Explanation
Use the cosine rule for vectors at any angle:
\( \mathrm{R^2 = F_1^2 + F_2^2 – 2F_1F_2\cos(180^\circ – \theta)} \)
Since the angle between vectors is 60∘ 60 ∘ , use the direct form:
\( \mathrm{R^2 = 20^2 + 15^2 + 2(20)(15)\cos60^\circ} \)
\( \mathrm{R^2 = 400 + 225 + 600(0.5)} \)
\( \mathrm{R^2 = 400 + 225 + 300 = 925} \)
\( \mathrm{R = \sqrt{925} \approx 30.4\ N} \)
Resultant ≈ \( \mathrm{30\ N} \).
