Edexcel A Level (IAL) Physics-1.7 Components of Velocity- Study Notes- New Syllabus

Independence of Vertical and Horizontal Motion in Projectiles

A projectile is any object moving through the air under the influence of gravity only (assuming no air resistance). A key idea in projectile motion is that the horizontal and vertical motions are independent of each other.

 Independence of Motion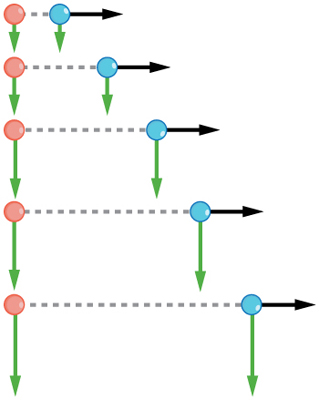

Horizontal motion:

• No horizontal forces → no horizontal acceleration.
• Horizontal velocity is constant.
• \( \mathrm{a_x = 0} \)
• \( \mathrm{v_x = u_x} \)
• \( \mathrm{x = u_x t} \)

Vertical motion:

• Only gravity acts vertically.
• Vertical acceleration is constant and downward.
• \( \mathrm{a_y = -g} \)
• Vertical motion follows SUVAT equations.

The two motions do not affect each other.

 Why Independence Occurs

• Gravity acts only vertically → cannot change horizontal velocity.
• No horizontal forces → cannot change vertical velocity.
• Mathematically, horizontal and vertical equations are separate and unrelated.
• The path of the projectile is the result of combining both independent motions.

Result: Projectile follows a parabolic path because horizontal motion is uniform while vertical motion is accelerated.

Projectile Motion

Projectile motion describes the path of an object moving under the influence of gravity only, with no air resistance. The object follows a curved (parabolic) path due to the independence of horizontal and vertical motion.

1. Key Principles of Projectile Motion

• Horizontal and vertical motions are independent.
• Gravity acts only vertically → causes vertical acceleration.
• No horizontal forces → horizontal velocity is constant.
• Path of projectile = parabola.
• SUVAT equations apply to the vertical direction only.

2. Horizontal Motion

No acceleration horizontally:

\( \mathrm{a_x = 0} \)

Horizontal velocity remains constant:

\( \mathrm{v_x = u_x} \)

Horizontal displacement:

\( \mathrm{x = u_x t} \)

3. Vertical Motion

Vertical motion behaves like motion under constant acceleration:

Acceleration due to gravity:

\( \mathrm{a_y = -g} \)

Vertical velocity:

\( \mathrm{v_y = u_y – gt} \)

Vertical displacement:

\( \mathrm{y = u_y t – \dfrac{1}{2}gt^2} \)

Time to reach maximum height:

\( \mathrm{t_{max} = \dfrac{u_y}{g}} \)

4. Angle of Projection

If a projectile is launched with speed u at angle θ:

• Horizontal component: \( \mathrm{u_x = u\cos\theta} \)
• Vertical component: \( \mathrm{u_y = u\sin\theta} \)

All projectile equations come from combining these components.

5. Range, Time of Flight and Maximum Height

Time of flight: (projectile lands at same vertical level)

\( \mathrm{T = \dfrac{2u\sin\theta}{g}} \)

Maximum height:

\( \mathrm{H = \dfrac{u^2\sin^2\theta}{2g}} \)

Horizontal range:

\( \mathrm{R = \dfrac{u^2\sin2\theta}{g}} \)

These apply only when landing height = launch height.

6. Projectile Motion from a Height (Horizontal Launch)

• Initial vertical velocity = 0
• Vertical displacement: \( \mathrm{y = -\dfrac{1}{2}gt^2} \)
• Time to hit ground: \( \mathrm{t = \sqrt{\dfrac{2h}{g}}} \)
• Range: \( \mathrm{R = u_x t} \)

7. Why Projectile Motion Is Parabolic

• Horizontal motion = constant velocity
• Vertical motion = constant acceleration
• Combining the two gives a quadratic curve → parabola