Edexcel A Level (IAL) Physics-1.9 Force & Acceleration- Study Notes- New Syllabus

Newton’s Laws of Motion and Using \( \mathrm{\sum F = ma} \)

Newton’s second law relates the resultant (net) force on an object to its mass and acceleration. This equation applies when the mass ( \mathrm{m} ) of the object is constant.

 Newton’s Second Law

Statement: Newton’s second law states that the rate of change of an object’s momentum is directly proportional to the net force applied to it and occurs in the same direction as the force.A more common and simplified statement is that the acceleration of an object is proportional to the resultant force acting on it and inversely proportional to its mass.

Mathematically:

\( \mathrm{\sum F = ma} \)

• \( \mathrm{\sum F} \) = net force acting on the object
• \( \mathrm{m} \) = mass (constant)
• \( \mathrm{a} \) = acceleration

Meaning: Acceleration occurs when there is a non-zero resultant force.

 Newton’s First Law

Statement: An object remains at rest, or moves at constant velocity, unless acted upon by a resultant force.

• Objects with \( \mathrm{a = 0} \) have zero resultant force: \( \mathrm{\sum F = 0} \)
• Applies to both objects at rest and objects with constant velocity.

 Using \( \mathrm{\sum F = ma} \)

Steps:

• • Draw the free-body diagram.
  • Select a direction as positive (usually direction of motion).
  • Resolve forces into components if necessary.
  • Apply Newton’s second law in each direction:

\( \mathrm{\sum F_x = ma_x} \)

\( \mathrm{\sum F_y = ma_y} \)

• Solve for the unknown quantity (acceleration, force, mass, etc.).

 Situations Where \( \mathrm{a = 0} \)

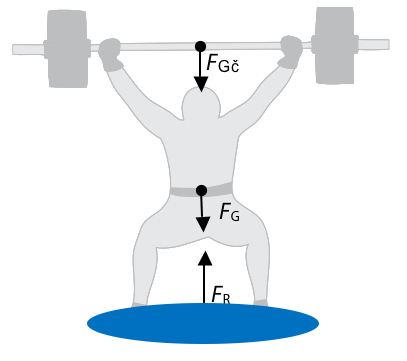
If \( \mathrm{a = 0} \), then:

\( \mathrm{\sum F = 0} \)

This is static or dynamic equilibrium.

• Object at rest → forces balanced.
• Object moving at constant velocity → forces still balanced.
• No resultant force → no acceleration.

 Terminal Velocity

Definition: Terminal velocity is the constant maximum velocity reached when the resistive forces equal the driving force so that the resultant force becomes zero.

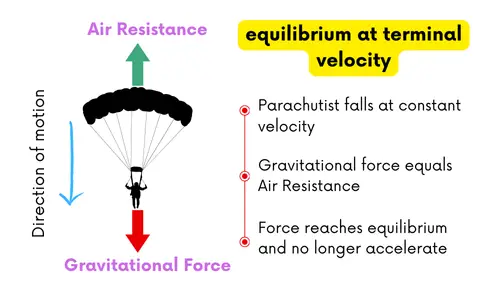
• Occurs in free fall when air resistance increases with speed.
• Eventually, weight = air resistance:

\( \mathrm{W = D} \)

• Resultant force becomes zero → \( \mathrm{a = 0} \).
• Velocity remains constant → terminal velocity.

Key idea: Terminal velocity is an application of Newton’s first law.

Common Situations Using ( \mathrm{\sum F = ma} )

• Objects pulled or pushed on a horizontal surface.
• Objects moving vertically under gravity + resistance.
• Motion on an incline (weight components).
• Tension problems involving masses and pulleys.
• Driving force vs resistive forces in cars.