Edexcel A Level (IAL) Physics-2.1 - 2.2 Properties of Waves and Wave Equation- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -2.1 – 2.2 Properties of Waves and Wave Equation- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -2.1 – 2.2 Properties of Waves and Wave Equation- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
Amplitude, Frequency, Period, Speed and Wavelength
This section defines the fundamental quantities used to describe waves and oscillations.
Amplitude
Amplitude is the maximum displacement of a point on a wave from its equilibrium (rest) position.
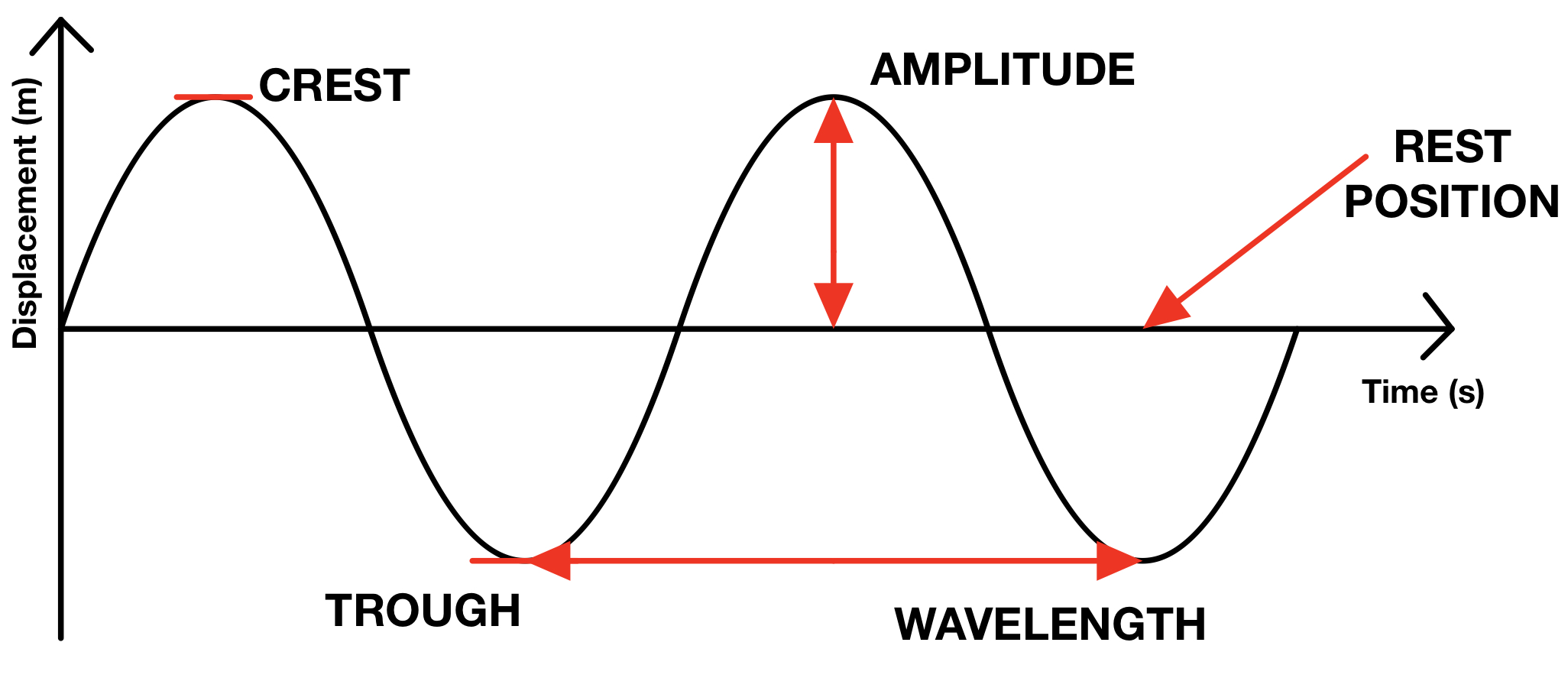
- Measured in metres (m).
- It determines the energy carried by the wave — larger amplitude → more energy.
- For sound: higher amplitude → louder sound.
- For light: higher amplitude → brighter light.
Frequency
Frequency is the number of complete oscillations or cycles per second.
\( f = \frac{1}{T} \)
- Measured in hertz (Hz).
- 1 Hz = 1 cycle per second.
- Higher frequency → more cycles per second.
Period
The period is the time taken for one complete wave cycle.
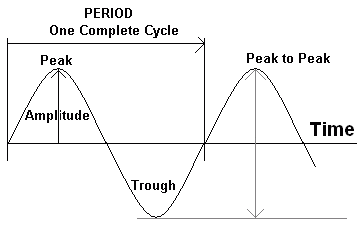
\( T = \frac{1}{f} \)
- Measured in seconds (s).
- Shorter period → higher frequency.
Wavelength
Wavelength is the distance between two consecutive points in phase on a wave, for example:
- Crest to crest
- Trough to trough
- Compression to compression (sound waves)
Symbol: \( \lambda \) (lambda), measured in metres (m).
Wave Speed
Wave speed is the distance travelled by the wave per unit time.
$ v = f\lambda $
- \( v \) = wave speed (m s⁻¹)
- \( f \) = frequency (Hz)
- \( \lambda \) = wavelength (m)
Wave speed depends on the medium, not on amplitude or frequency.
Summary of Key Relationships
- \( v = f\lambda \)
- \( T = \frac{1}{f} \)
- Amplitude affects energy but not speed.
- Frequency and wavelength change when medium changes, but speed follows the medium’s properties.
Example (Easy)
A wave has a frequency of \( 5\, \mathrm{Hz} \). What is its period?
▶️ Answer / Explanation
\( T = \frac{1}{f} = \frac{1}{5} = 0.2\, \mathrm{s} \)
Example (Medium)
A water wave has a wavelength of \( 0.8\, \mathrm{m} \) and a frequency of \( 2.5\, \mathrm{Hz} \). Find its speed.
▶️ Answer / Explanation
\( v = f\lambda = 2.5 \times 0.8 = 2.0\, \mathrm{m\,s^{-1}} \)
Example (Hard)
A sound wave travels at \( 340\, \mathrm{m\,s^{-1}} \) and has a frequency of \( 1700\, \mathrm{Hz} \). Calculate its wavelength.
▶️ Answer / Explanation
\( \lambda = \frac{v}{f} = \frac{340}{1700} = 0.20\, \mathrm{m} \)
Using the Wave Equation \( v = f\lambda \)
The wave equation connects the speed of a wave to its frequency and wavelength. It is one of the most important equations in wave physics and applies to all types of waves (sound, water, light, electromagnetic waves, etc.).
The Wave Equation
The speed of a wave is given by:
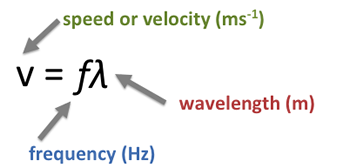
- \( v \) = wave speed (m s⁻¹)
- \( f \) = frequency (Hz)
- \( \lambda \) = wavelength (m)
This means:
- Higher frequency → shorter wavelength (if speed is constant).
- Longer wavelength → lower frequency.
- Speed of a wave depends on the medium, not on amplitude.
Rearranged Forms
- Find wavelength:
\( \lambda = \dfrac{v}{f} \)
- Find frequency:
\( f = \dfrac{v}{\lambda} \)
- Find speed:
\( v = f\lambda \)
Notes on Using the Wave Equation
- Units must be consistent (speed in m/s, wavelength in m).
- Only use \( v = f\lambda \) when wave behaviour is steady and medium is uniform.
- Electromagnetic waves in vacuum: \( v = c = 3.00\times10^8 \,\mathrm{m\,s^{-1}} \).
- Sound speed varies with medium (air ≈ 340 m/s).
Example (Easy)
A wave has frequency \( 10\, \mathrm{Hz} \) and wavelength \( 0.5\, \mathrm{m} \). Calculate its speed.
▶️ Answer / Explanation
\( v = f\lambda = 10 \times 0.5 = 5\, \mathrm{m\,s^{-1}} \)
Example (Medium)
The speed of a water wave is \( 3.2\, \mathrm{m\,s^{-1}} \) and its wavelength is \( 0.80\, \mathrm{m} \). Find the frequency.
▶️ Answer / Explanation
\( f = \frac{v}{\lambda} = \frac{3.2}{0.80} = 4.0\, \mathrm{Hz} \)
Example (Hard)
A sound wave in air has a frequency of \( 1700\, \mathrm{Hz} \). If the speed of sound is \( 340\, \mathrm{m\,s^{-1}} \), calculate its wavelength.
▶️ Answer / Explanation
\( \lambda = \frac{340}{1700} = 0.20\, \mathrm{m} \)