Edexcel A Level (IAL) Physics-2.10 Wave Speed on a Stretched Spring- Study Notes- New Syllabus

Speed of a Transverse Wave on a String \( v = \sqrt{\dfrac{T}{\mu}} \)

This formula gives the speed of a transverse wave travelling along a stretched string or wire. It depends on how tight the string is and how much mass it has per unit length.

The Wave Speed Formula

The speed of a transverse wave on a string is: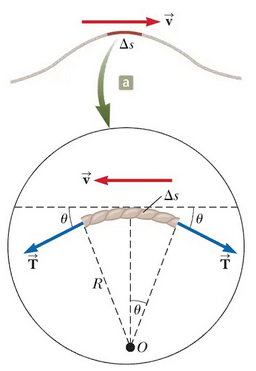

$ v = \sqrt{\frac{T}{\mu}} $

• \( v \) = wave speed (m s⁻¹)
• \( T \) = tension in the string (N)
• \( \mu \) = mass per unit length of the string (kg m⁻¹)

Meaning:

• Increasing tension → increases wave speed.
• Increasing mass per unit length → decreases wave speed.
• Speed does NOT depend on the amplitude or frequency of the oscillations.

Understanding Mass per Unit Length \( \mu \)

\( \mu \) tells us how “heavy” a string is for each metre of length. It is calculated by:

$ \mu = \frac{m}{L} $

• \( m \) = mass of the string (kg)
• \( L \) = length of the string (m)

Thicker or denser strings have larger \( \mu \) → waves travel more slowly.

Physical Interpretation

• A tighter string pulls the wave forward faster → larger \( T \).
• A heavier string resists acceleration → larger \( \mu \).
• The formula resembles Newton’s second law: higher tension provides more force; higher mass per metre resists motion.

 Applications

• Vibrating strings on musical instruments.
• Laboratory experiments for measuring tension & string density.
• Understanding harmonics and standing waves on strings.
• Stringed resonance tubes in physics experiments.

Using the Formula Correctly

• Always convert mass of string to kilograms.
• Ensure \( \mu \) is in kg/m.
• Tension must be measured in newtons.
• Wave speed depends only on string properties — not on the driving frequency.