Edexcel A Level (IAL) Physics-2.14 Critical Angle- Study Notes- New Syllabus

Critical Angle and Total Internal Reflection \( \sin C = \frac{1}{n} \)

When light travels from a denser medium (higher refractive index) to a less dense medium (lower refractive index), the angle of refraction increases. Beyond a certain incident angle, refraction no longer occurs — the light is totally reflected. This incident angle is the critical angle.

What is the Critical Angle?

The critical angle \( C \) is the angle of incidence in a denser medium for which the angle of refraction is \( 90^\circ \).

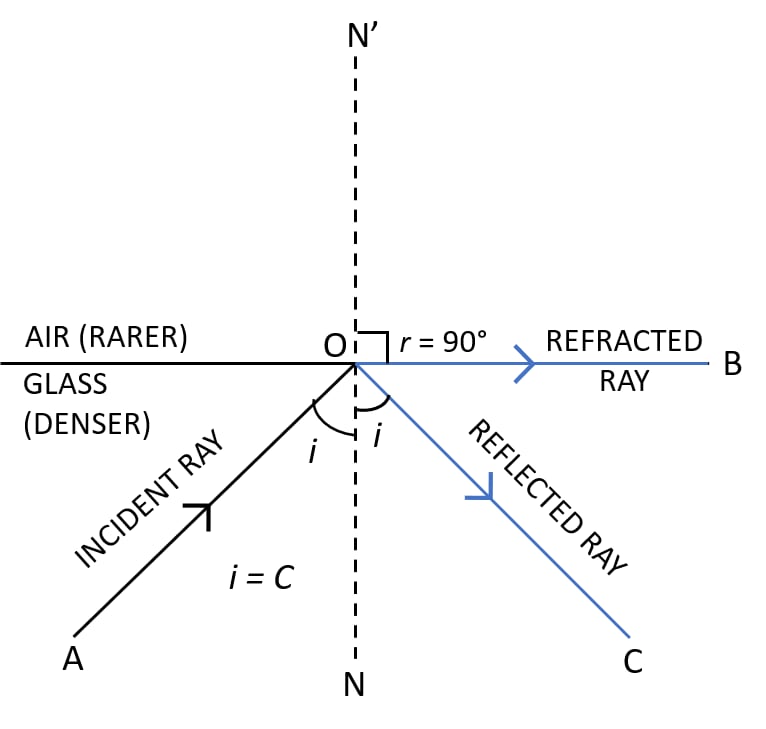
Occurs only when:

• \( n_1 > n_2 \) (light going from denser to rarer medium)
• Refracted ray travels along the boundary

Formula for the Critical Angle

From Snell’s law:

$ n_1 \sin C = n_2 \sin 90^\circ $

Since \( \sin 90^\circ = 1 \), and if the less dense medium is air \( (n_2 = 1) \):

$ \sin C = \frac{1}{n} $

• \( C \) = critical angle
• \( n \) = refractive index of the denser medium

Total Internal Reflection (TIR)

Total internal reflection occurs when:

• Light travels from higher \( n \) → lower \( n \)
• Angle of incidence > critical angle

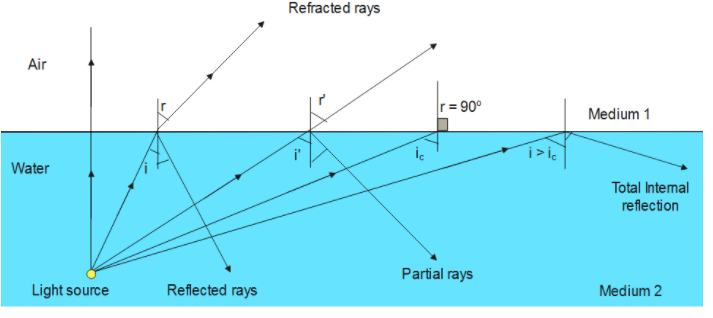
Effects:

• No refracted ray
• All light is reflected back into the denser medium
• Reflection obeys the normal law of reflection

Applications:

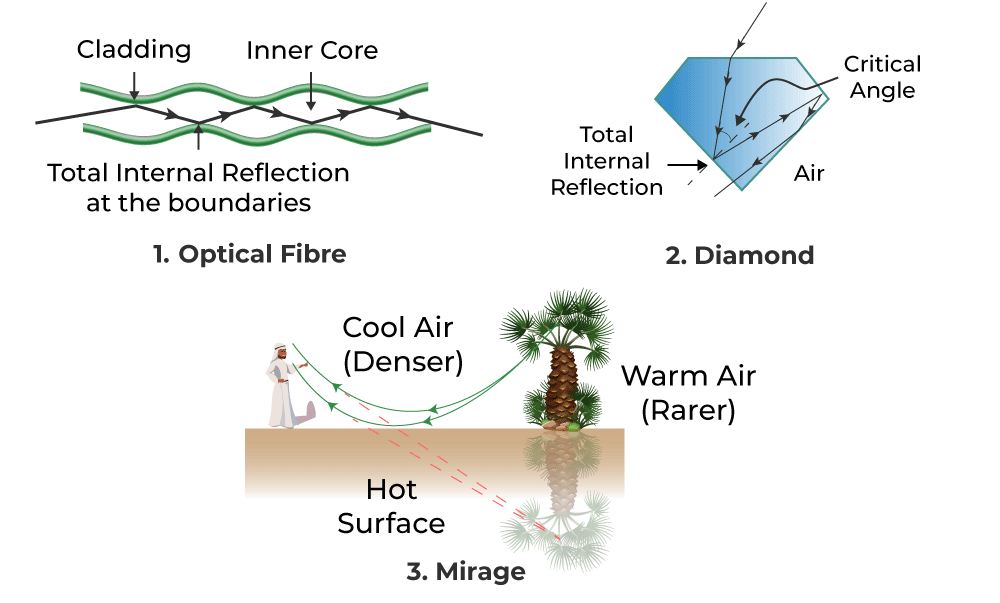
• Optical fibres
• Endoscopes
• Prism binoculars
• Diamond sparkle (high refractive index → small critical angle)

Using \( \sin C = \frac{1}{n} \)

Given the refractive index of a medium, the critical angle can be calculated by:

$ C = \sin^{-1}\left(\frac{1}{n}\right) $

Notes:

• Applies only when light is leaving the denser medium.
• If \( n \leq 1 \), no critical angle exists.
• Higher refractive index → smaller critical angle.