Edexcel A Level (IAL) Physics-2.15 Total Internal Reflection- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -2.15 Total Internal Reflection- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -2.15 Total Internal Reflection- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
- be able to predict whether total internal reflection will occur at an interface
Predicting Whether Total Internal Reflection Will Occur
Total Internal Reflection (TIR) is a phenomenon that occurs when a wave (usually light) reflects completely back into a denser medium instead of refracting into a less dense medium. To determine whether TIR will occur, two key conditions must be satisfied.
Conditions for Total Internal Reflection
TIR occurs only when both of the following are true:
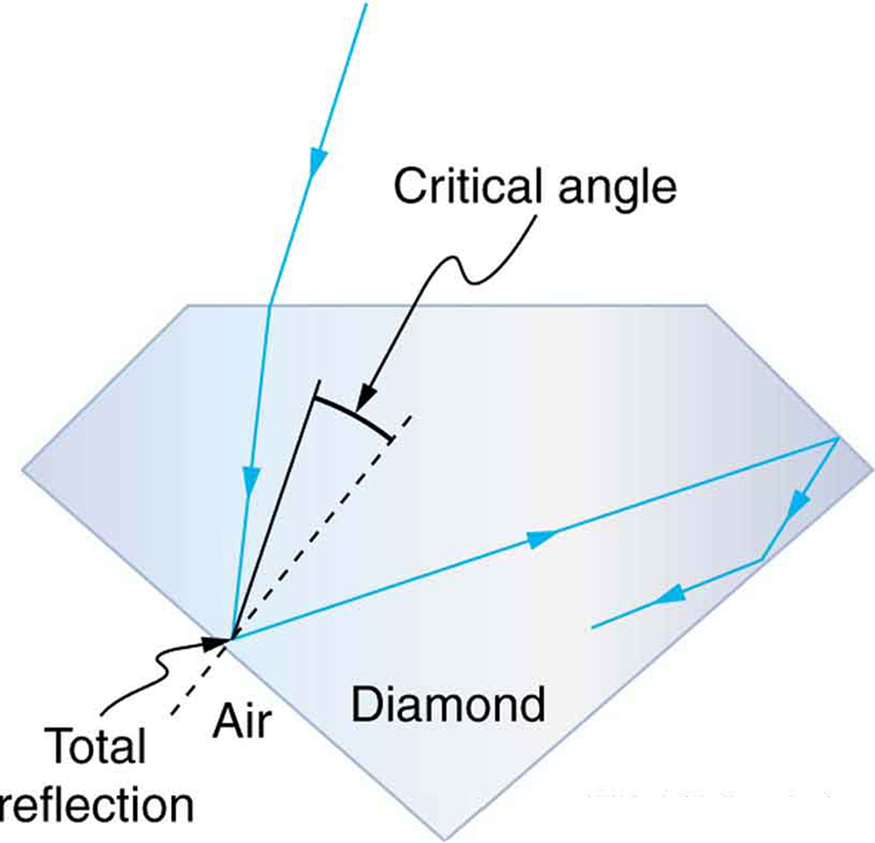
- Condition 1: The wave must travel from a medium with higher refractive index to one with lower refractive index.
i.e., \( n_{\text{incident}} > n_{\text{refracted}} \)
- Condition 2: The angle of incidence must be greater than the critical angle \( C \).
The critical angle is given by:
$ \sin C = \frac{1}{n} $
How to Predict TIR Step-by-Step
- Identify which medium is denser (higher refractive index).
- Check if the wave is travelling from higher \( n \) → lower \( n \).
If not → TIR cannot occur. - Calculate the critical angle using:
$ C = \sin^{-1}\left(\frac{1}{n}\right) $
(Assuming the other medium is air; if not, use Snell’s law).
- Compare the incident angle \( \theta_i \) to the critical angle.
- If \( \theta_i < C \) → refraction occurs.
- If \( \theta_i = C \) → refracted ray grazes the boundary.
- If \( \theta_i > C \) → total internal reflection occurs.
Visual Summary
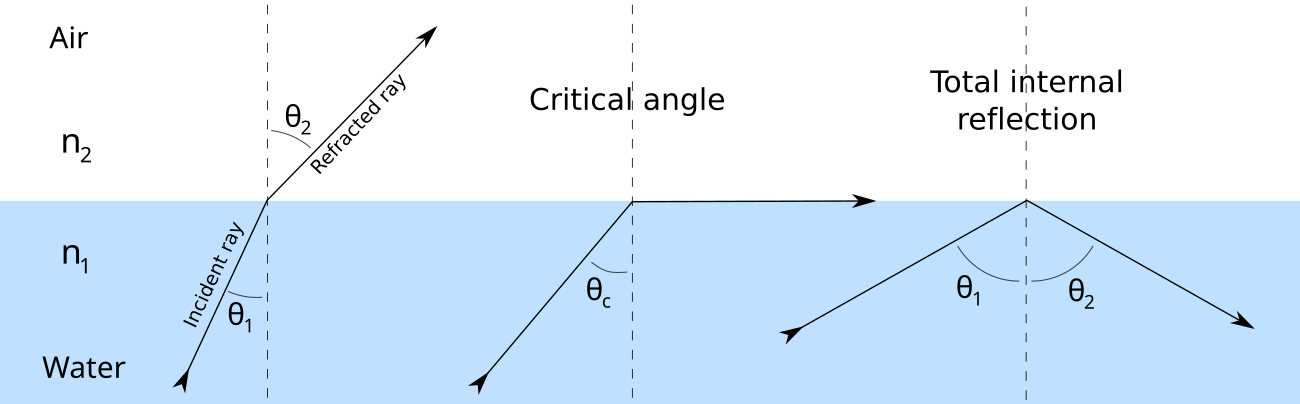
- If light enters a denser medium → No TIR possible.
- If light leaves a denser medium but \( \theta_i < C \) → Refraction + partial reflection.
- If light leaves a denser medium and \( \theta_i > C \) → 100% reflection (TIR).
Example (Easy)
Light travels from glass (\( n = 1.50 \)) to air. Incident angle = \( 20^\circ \). Will total internal reflection occur?
▶️ Answer / Explanation
Step 1: Calculate critical angle:
$ \sin C = \frac{1}{1.50} = 0.667 $ $ C = \sin^{-1}(0.667) \approx 41.8^\circ $
Step 2: Compare angles:
- Incident angle = \( 20^\circ \)
- Critical angle = \( 42^\circ \)
Since \( 20^\circ < 42^\circ \), no TIR occurs.
Example (Medium)
A ray in diamond (\( n = 2.42 \)) strikes the boundary with air at \( 30^\circ \). Predict whether TIR occurs.
▶️ Answer / Explanation
Step 1: Find critical angle.
$ \sin C = \frac{1}{2.42} = 0.413 $ $ C = \sin^{-1}(0.413) \approx 24.4^\circ $
Step 2: Compare angles:
- Incident angle = \( 30^\circ \)
- Critical angle = \( 24.4^\circ \)
Since \( 30^\circ > 24.4^\circ \), TIR occurs.
Example (Hard)
A ray passes from glass (\( n_1 = 1.60 \)) into water (\( n_2 = 1.33 \)) with incident angle \( 50^\circ \). Will total internal reflection occur?
▶️ Answer / Explanation
Step 1: Use Snell’s law for critical angle:
$ n_1 \sin C = n_2 \sin 90^\circ = n_2 $ $ \sin C = \frac{1.33}{1.60} = 0.831 $ $ C = \sin^{-1}(0.831) \approx 56.3^\circ $
Step 2: Compare angles:
- Incident angle = \( 50^\circ \)
- Critical angle = \( 56.3^\circ \)
Since \( 50^\circ < 56.3^\circ \), TIR does NOT occur.
