Edexcel A Level (IAL) Physics-2.16 Measuring Refractive Index- Study Notes- New Syllabus

Measuring the Refractive Index of a Solid Material

To measure the refractive index of a solid, we normally use one of the following: (1) Snell’s Law method using a rectangular or semicircular block, or (2) Critical angle method using a prism.

Both methods rely on the definition of refractive index: 

$ n = \frac{\sin\theta_1}{\sin\theta_2} = \frac{c}{v} $

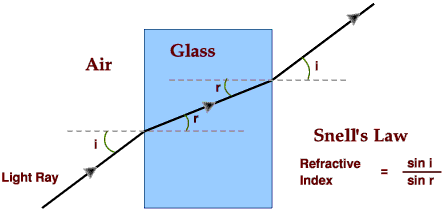
 Method 1: Using Snell’s Law (Rectangular Glass Block)

This is the most common laboratory method.

Apparatus:

• Rectangular glass block
• Ray box or laser
• Protractor
• Paper and pencil
• Pins (for ray tracing)

Procedure:

1. Place the rectangular block on paper and trace around it.
2. Shine a ray into the block at different angles of incidence.
3. Trace the incident and emergent rays.
4. Measure:
   • angle of incidence \( \theta_1 \)
   • angle of refraction \( \theta_2 \)
5. Repeat for a range of angles.
6. Plot:
   

   \( \sin\theta_1 \) (y-axis) vs \( \sin\theta_2 \) (x-axis)

7. The gradient = refractive index \( n \).

Using Snell’s law:

$ n = \frac{\sin\theta_1}{\sin\theta_2} $

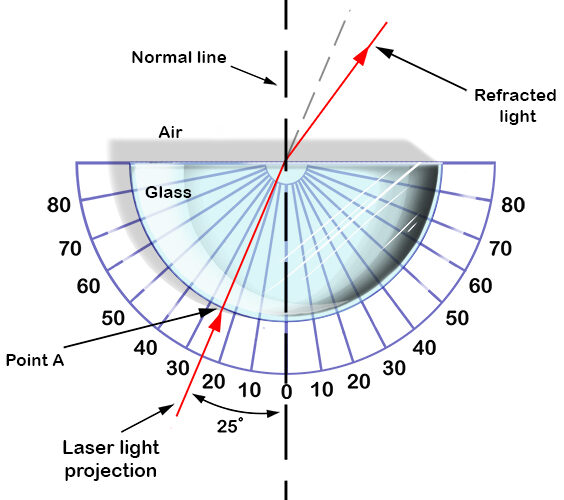
 Method 2: Using the Critical Angle (Prism or Block)

Useful when the material has a critical angle that can be measured directly.

Apparatus:

• Glass or Perspex prism
• Laser or ray box
• Protractor

Procedure:

1. Shine a ray inside the prism so it meets the boundary with air.
2. Increase the angle of incidence until the refracted ray just disappears — the ray emerges along the boundary.
3. Measure this angle → the critical angle \( C \).
4. Use:
   

   $ \sin C = \frac{1}{n} $

5. Rearrange:
   

   $ n = \frac{1}{\sin C} $

Notes and Tips

• Ensure boundaries are clean and dry.
• Use a fine, narrow laser beam for accuracy.
• Measure angles carefully with a protractor.
• Take multiple measurements and average them.
• Use a semicircular block to avoid refraction on entry.

Why semicircular blocks are helpful?

• The entry surface is curved → ray enters normal to the surface → no refraction on entry.
• This isolates refraction only at the flat face.