Edexcel A Level (IAL) Physics-2.18 - 2.19 Diffraction and Diffraction Grating Equation- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -2.18 – 2.19 Diffraction and Diffraction Grating Equation- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -2.18 – 2.19 Diffraction and Diffraction Grating Equation- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
Diffraction and Huygens’ Construction
Diffraction is the spreading of waves when they pass through a gap or move around an obstacle. It is a fundamental wave phenomenon that occurs with all types of waves — water waves, sound waves, light waves, and even matter waves.
What Is Diffraction?
- When a wave passes through a slit or past the edge of an object, it spreads out.
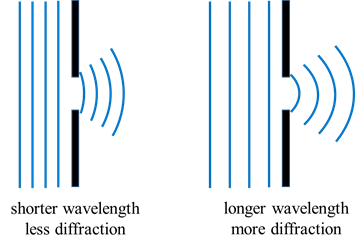
- Diffraction is most noticeable when the size of the slit or obstacle is comparable to the wavelength.
- Light diffracts very little through large slits because its wavelength is extremely small.
Key idea: Greater spreading occurs when slit width ≈ wavelength.
Huygens’ Construction (Huygens’ Principle)
Huygens’ principle states:
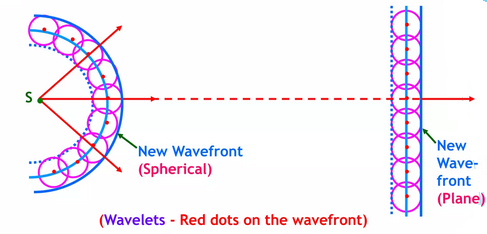
- Every point on a wavefront acts as a source of secondary spherical wavelets.
- The new wavefront is the surface tangent to all these secondary wavelets.
This helps explain how waves change direction when encountering a boundary.
Using Huygens’ Principle to Explain Diffraction
(a) Wave Meets a Slit
- Each point across the slit acts as a source of secondary wavelets.
- These wavelets spread out in all forward directions.
- The overlapping of these wavelets forms a curved wavefront after the slit.
- For a narrow slit (width ≈ wavelength), the wavefront becomes almost circular → strong diffraction.
(b) Wave Meets an Obstacle
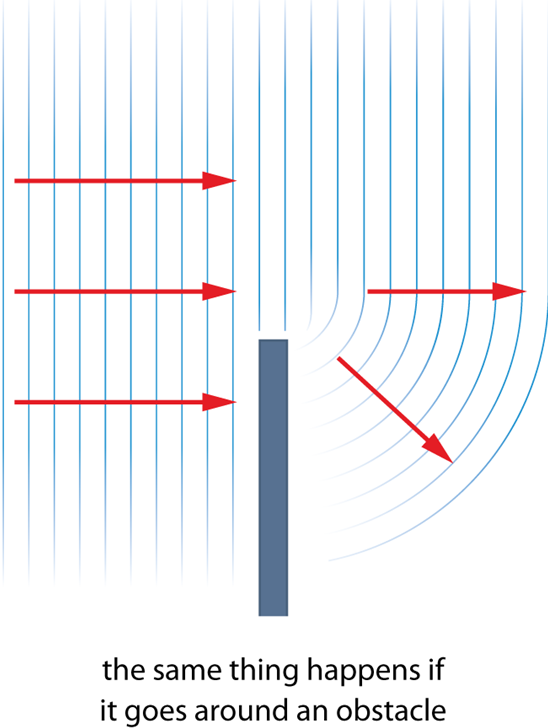
- The wavefront hits the obstacle and is blocked except at the edges.
- Edges behave like point sources of new wavelets.
- These edge-originating wavelets spread into the shadow region.
Conclusion: Diffraction occurs because edge points behave as new sources of waves.
Factors Affecting Diffraction
- Wavelength:
- Longer wavelength → more diffraction.
- Sound (large wavelength) diffracts well; light (small wavelength) diffracts poorly.
- Slit Width:
- Wide slit ≫ wavelength → very little diffraction.
- Narrow slit ≈ wavelength → strong spreading.
- Obstacle Size:
- Large obstacle → small edge diffraction.
- Obstacle size ≈ wavelength → noticeable bending.
Importance of Diffraction
- Essential for understanding interference patterns.
- Used in diffraction gratings and spectroscopy.
- Explains why sound can be heard around corners.
- Explains resolution limits of microscopes and telescopes.
Example (Easy)
Why does sound bend around corners but light does not?
▶️ Answer / Explanation
- Sound has a very large wavelength (≈ 1 m).
- Building doorways and corners have size ≈ wavelength → strong diffraction.
- Light has a very small wavelength (≈ \( 5 \times 10^{-7} \) m) → barely diffracts.
Example (Medium)
A slit has width equal to the wavelength of a wave. Describe what happens as the wave passes through the slit using Huygens’ principle.
▶️ Answer / Explanation
Each point on the slit behaves as a source of secondary wavelets. These wavelets spread in all forward directions, overlapping to produce a nearly circular wavefront. This results in strong diffraction.
Example (Hard)
Explain why diffraction decreases when slit width becomes much larger than wavelength.
▶️ Answer / Explanation
- A wider slit contains many secondary sources (according to Huygens).
- Most of these are in the interior → their wavelets interfere and reinforce a forward-moving plane wave.
- Only the edge sources produce spreading, but their effect becomes small compared to interior contributions.
- Thus, the outgoing wave remains almost straight → little diffraction.
Diffraction Grating: Using the Equation \( n\lambda = d\sin\theta \)
A diffraction grating consists of many equally spaced slits that diffract light and produce sharp interference maxima. The condition for maxima is given by the diffraction grating equation.
Diffraction Grating Formula
The angles at which bright fringes (maxima) occur are found using:
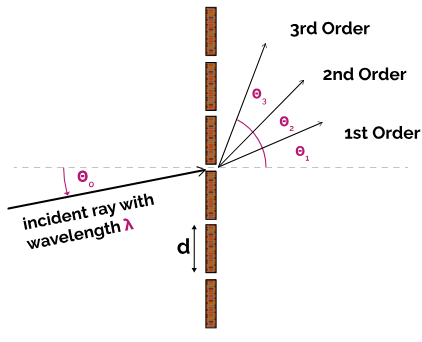
\( n\lambda = d\sin\theta \)
- \( n \) = order of maximum (0, 1, 2, 3 …)
- \( \lambda \) = wavelength of light (m)
- \( d \) = grating spacing (m)
- \( \theta \) = angle of diffraction (from normal)
Meaning: Constructive interference occurs when the path difference between adjacent slits equals an integer multiple of wavelength.
Grating Spacing \( d \)
If the grating has \( N \) lines per metre, then:
\( d = \dfrac{1}{N} \)
Example: 600 lines per mm → \( N = 600 \times 10^3 = 6.0\times10^5\ \mathrm{m^{-1}} \) → \( d = \dfrac{1}{6.0\times10^5} \)
Features of Diffraction Gratings
- Produce very sharp, bright maxima (better than double slits)
- Widely used in spectroscopy
- Higher orders give larger angles
- Maximum order when \( \sin\theta = 1 \), so:
\( n_{\text{max}} = \dfrac{d}{\lambda} \)
How to Use the Formula
- Find \( d \) from number of lines per metre.
- Choose the order \( n \) (e.g., 1st, 2nd, 3rd).
- Substitute wavelength \( \lambda \).
- Solve for the angle \( \theta \) or wavelength depending on the question.
Example (Easy)
A grating has 500 lines per mm. Find the slit spacing \( d \).
▶️ Answer / Explanation
500 lines/mm = \( 500 \times 10^3 = 5.0\times10^5\ \mathrm{m^{-1}} \)
\( d = \dfrac{1}{5.0\times10^5} = 2.0\times10^{-6}\ \mathrm{m} \)
Example (Medium)
White light of wavelength \( \lambda = 600\ \mathrm{nm} \) falls on a grating with spacing \( d = 2.0\times10^{-6}\ \mathrm{m} \). Find the first-order diffraction angle.
▶️ Answer / Explanation
Using \( n\lambda = d\sin\theta \):
\( 1 \times 600\times10^{-9} = 2.0\times10^{-6}\sin\theta \)
\( \sin\theta = \dfrac{600\times10^{-9}}{2.0\times10^{-6}} = 0.300 \)
\( \theta = \sin^{-1}(0.300) \approx 17.5^\circ \)
Example (Hard)
Light of wavelength \( 520\ \mathrm{nm} \) is used with a diffraction grating of spacing \( 1.80\times10^{-6}\ \mathrm{m} \). What is the highest possible order visible?
▶️ Answer / Explanation
Condition for maximum order:
\( n_{\text{max}} = \dfrac{d}{\lambda} \)
\( n_{\text{max}} = \dfrac{1.80\times10^{-6}}{520\times10^{-9}} = 3.46 \)
The highest whole number ≤ 3.46 is:
n = 3
Maximum observable order = 3