Edexcel A Level (IAL) Physics-2.21 The Wave Nature of Electrons- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -2.21 The Wave Nature of Electrons- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -2.21 The Wave Nature of Electrons- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
Electron Diffraction as Evidence for the Wave Nature of Electrons
Diffraction is a property associated with waves, not particles. If electrons show diffraction patterns, this means electrons must behave like waves. This is a key idea in quantum mechanics, known as wave–particle duality.
Key Idea: Waves Diffract, Particles Do Not
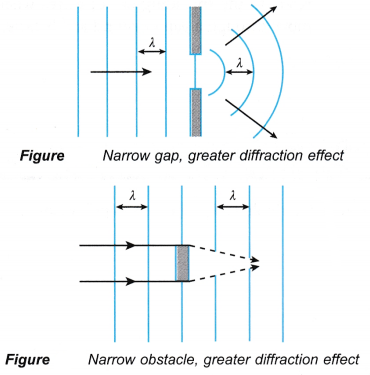
- Diffraction occurs when a wave passes through a narrow gap or around an obstacle.
- Only waves spread out or form interference fringes.
- If electrons (which are particles) show diffraction, they must also behave like waves.
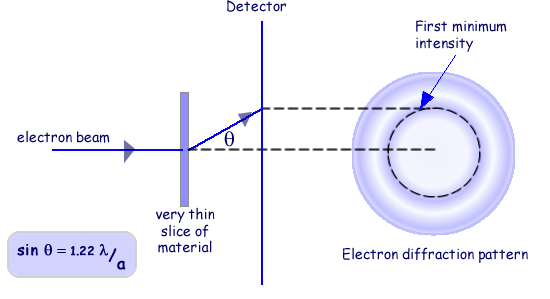
Electron Diffraction Experiment
- Electrons are accelerated through a potential difference.
- They are directed at a thin polycrystalline graphite film.
- The small spacing between graphite atoms (~ \( 10^{-10}\ \mathrm{m} \)) acts like a diffraction grating.
- A fluorescent screen detects where electrons land.
Observation: Electrons produce circular diffraction rings — exactly like X-rays.
Conclusion: Electrons undergo diffraction → electrons behave like waves.
Explanation Using de Broglie Wavelength
Louis de Broglie proposed that particles have a wavelength given by:
\( \lambda = \dfrac{h}{p} = \dfrac{h}{mv} \)
- \( \lambda \) = wavelength of electron
- \( h \) = Planck’s constant
- \( p \) = momentum
When electron wavelength is similar to atomic spacing (≈ \( 10^{-10}\ \mathrm{m} \)), diffraction is observed.
Effect of Accelerating Voltage
- Higher accelerating voltage → electrons gain more speed → larger momentum → smaller wavelength.
- Smaller wavelength → less diffraction (rings move inward).
This matches the equation \( \lambda = \dfrac{h}{mv} \), providing strong evidence for wave behaviour.
Why Electron Diffraction Proves Wave Nature
- Electrons create a diffraction pattern only waves can produce.
- Changing accelerating voltage changes the pattern exactly as wave theory predicts.
- The spacing of diffraction rings matches the de Broglie equation.
Thus, electrons must have wavelength → electrons behave as waves.
Example (Easy)
Why does observing diffraction patterns from electrons indicate that electrons behave like waves?
▶️ Answer / Explanation
Only waves can diffract. Since electrons produce diffraction patterns, they must have wave-like properties.
Example (Medium)
What happens to the diffraction pattern when the accelerating voltage of electrons is increased?
▶️ Answer / Explanation
- Higher voltage → higher electron speed.
- Momentum increases → de Broglie wavelength decreases.
- Smaller wavelength → diffraction rings move closer together (reduced diffraction).
Example (Hard)
An electron beam shows a strong diffraction ring when the accelerating voltage is 2 kV. Explain why the diffraction pattern becomes faint or disappears when the voltage increases to 20 kV.
▶️ Answer / Explanation
- Increasing voltage increases kinetic energy and velocity.
- Momentum increases → wavelength becomes much smaller:
\( \lambda = \dfrac{h}{p} \)
- If \( \lambda \) becomes much smaller than atomic spacing (~\( 10^{-10}\ \mathrm{m} \)),
- Diffraction becomes negligible → rings become faint or vanish.
Thus the pattern disappears because the electron wavelength is too small to diffract.