Edexcel A Level (IAL) Physics-2.25 - 2.26 Wave–Particle Duality and Energy of a Photon- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -2.25 – 2.26 Wave–Particle Duality and Energy of a Photon- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -2.25 – 2.26 Wave–Particle Duality and Energy of a Photon- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
- understand how the behaviour of electromagnetic radiation can be described in terms of a wave model and a photon model, and how these models developed over time
- be able to use the equation \(E=hf\), that relates the photon energy to the wave frequency
The Wave Model and Photon Model of Electromagnetic Radiation
Electromagnetic (EM) radiation can be described using two complementary models:
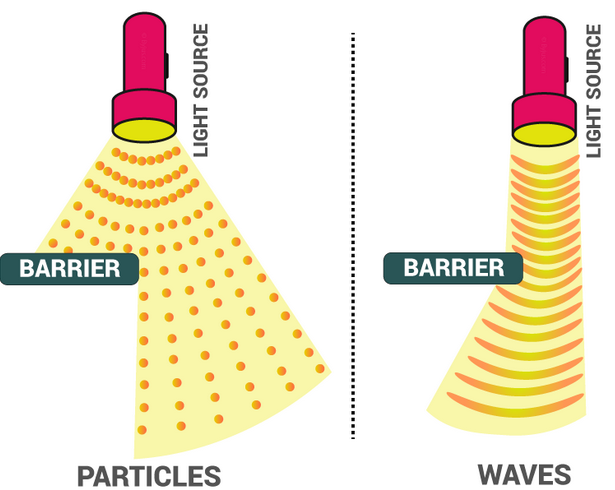
- A wave model — explains diffraction, interference, polarisation, and refraction.
- A photon (particle) model — explains the photoelectric effect, emission spectra, and interactions at the quantum level.
Modern physics shows that electromagnetic radiation behaves as both a wave and a particle, depending on the situation. This is known as wave–particle duality.
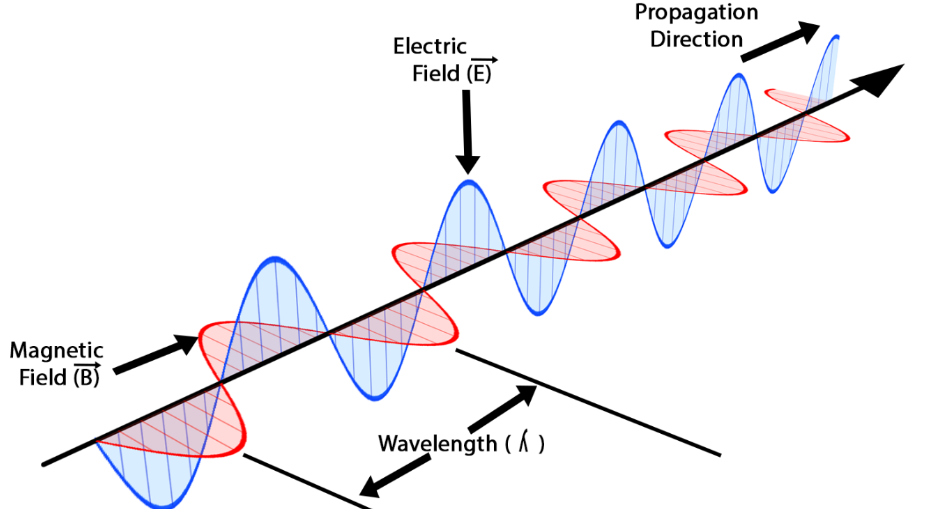
The Wave Model
The wave model treats EM radiation as a continuous oscillating electric and magnetic field.
- Predicted by Maxwell’s equations (19th century).

- Explains:
- Interference
- Diffraction
- Polarisation
- Reflection and refraction
- Travels at speed \( c = 3.0\times10^{8}\ \mathrm{m\,s^{-1}} \).
- Each wave has:
- Wavelength \( \lambda \)
- Frequency \( f \)
- Speed \( v = f\lambda \)
Evidence for the Wave Model:

- Young’s double-slit experiment showed interference fringes.
- Diffraction and polarisation only occur for waves.
- These results strongly confirmed the wave nature of light.
The Photon (Particle) Model
The photon model treats EM radiation as a stream of small packets of energy called photons.

\( E = hf \)
- \( E \) = energy of a photon
- \( h \) = Planck’s constant
- \( f \) = frequency of radiation
Reasons for the Photon Model:

- Photoelectric effect: Light ejects electrons from metal only if frequency exceeds threshold → cannot be explained by wave theory.
- Discrete atomic spectra: Light emitted in quantised packets → photons.
- Compton scattering: X-rays scatter like particles colliding with electrons.
Thus, EM radiation must also behave as particles.
How the Models Developed Over Time
- 17th century: Newton proposed a particle theory of light; Huygens proposed a wave theory.
- 19th century: Wave theory confirmed by diffraction, interference; Maxwell shows EM waves exist.
- Early 20th century:
- Planck introduces quantisation of energy.
- Einstein explains photoelectric effect using photons.
- de Broglie proposes wave–particle duality for matter.
- Modern view: Light is neither just a wave nor just a particle — it exhibits both natures.
| Use the Wave Model For | Use the Photon Model For |
|---|---|
| Polarisation | Photoelectric effect |
| Diffraction | X-ray production |
| Interference | Absorption or emission of energy by atoms |
| Refraction | Gamma-ray interactions |
Summary: Wave–Particle Duality
- Light behaves like a wave when travelling or interacting with slits/barriers.
- Light behaves like a stream of particles when interacting with electrons or matter.
- Both models are needed for a complete description of EM radiation.
Example (Easy)
Which model explains diffraction and interference?
▶️ Answer / Explanation
The wave model explains both diffraction and interference. These are wave behaviours and cannot be explained by the photon model.
Example (Medium)
Light of frequency \( f \) has energy \( E = hf \). If the frequency increases, what happens to the photon energy and why?
▶️ Answer / Explanation
- Photon energy increases because \( E \propto f \).
- Higher-frequency light (e.g., UV) delivers more energy per photon.
Example (Hard)
Why can light eject electrons from a metal (photoelectric effect) even at low intensity, provided its frequency is high enough?
▶️ Answer / Explanation
- In the photon model, each photon carries energy \( E = hf \).
- If \( f \) is above the threshold frequency, a single photon can eject an electron regardless of intensity.
- Low intensity means fewer photons, but each photon still has the same energy.
- Wave theory cannot explain this — but photon theory can.
Photon Energy and the Equation \( E = hf \)
Electromagnetic radiation can behave as particles called photons. Each photon carries energy that depends on the frequency of the radiation. This relationship is given by the photon energy equation:
\( E = hf \)
- \( E \) = energy of one photon (J)
- \( h \) = Planck’s constant \( 6.63\times10^{-34}\ \mathrm{J\,s} \)
- \( f \) = frequency of radiation (Hz)
Meaning of the Equation
- Photon energy is directly proportional to wave frequency.
- Higher-frequency radiation (e.g., UV, X-ray, gamma) → more energy per photon.
- Lower-frequency radiation (e.g., radio, microwaves) → less energy per photon.
- Wavelength and frequency are related by:
\( c = f\lambda \)
Using this, an alternative form is:
\( E = \dfrac{hc}{\lambda} \)
Why Photon Energy Matters
- Determines whether the radiation can eject electrons (photoelectric effect).
- Explains colours produced by atoms (emission spectra).
- Controls ionisation ability of EM waves.
- Important in lasers, LEDs, X-ray machines, and gamma radiation physics.
Frequency, Wavelength, and Energy
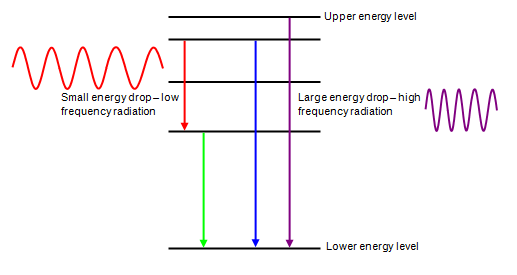
- Shorter wavelength → higher frequency → higher photon energy.
- Longer wavelength → lower frequency → lower photon energy.
Examples of photon energy levels:
- Radio waves: extremely low energy
- Visible light: moderate energy
- Ultraviolet: high energy
- X-rays and gamma rays: very high energy
Units
- Photon energy usually in joules (J).
- Sometimes converted to electronvolts:
\( 1\ \mathrm{eV} = 1.6\times10^{-19}\ \mathrm{J} \)
Example (Easy)
Calculate the energy of a photon of frequency \( 5.0\times10^{14}\ \mathrm{Hz} \).
▶️ Answer / Explanation
\( E = hf = (6.63\times10^{-34})(5.0\times10^{14}) = 3.32\times10^{-19}\ \mathrm{J} \)
Example (Medium)
Find the energy of a photon of wavelength \( 450\ \mathrm{nm} \).
▶️ Answer / Explanation
Step 1: Convert wavelength.
\( 450\ \mathrm{nm} = 450\times10^{-9}\ \mathrm{m} \)
Step 2: Use \( E = \dfrac{hc}{\lambda} \).
\( E = \dfrac{(6.63\times10^{-34})(3.0\times10^{8})}{450\times10^{-9}} = 4.42\times10^{-19}\ \mathrm{J} \)
Example (Hard)
An X-ray photon has an energy of \( 3.0\times10^{-15}\ \mathrm{J} \). Find its frequency and wavelength.
▶️ Answer / Explanation
Step 1: Use \( E = hf \) to find frequency.
\( f = \dfrac{E}{h} = \dfrac{3.0\times10^{-15}}{6.63\times10^{-34}} = 4.52\times10^{18}\ \mathrm{Hz} \)
Step 2: Use \( c = f\lambda \).
\( \lambda = \dfrac{c}{f} = \dfrac{3.0\times10^{8}}{4.52\times10^{18}} = 6.64\times10^{-11}\ \mathrm{m} \)
Wavelength = \( 6.6\times10^{-11}\ \mathrm{m} \) (X-ray range)