Edexcel A Level (IAL) Physics-2.27 - 2.28 The Photoelectric Effect and Photoelectric Equation- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -2.27 – 2.28 The Photoelectric Effect and Photoelectric Equation- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -2.27 – 2.28 The Photoelectric Effect and Photoelectric Equation- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
Photon Absorption and Photoelectron Emission
The photoelectric effect describes how a photon (a particle of electromagnetic radiation) can transfer its energy to an electron in a material. If the photon has enough energy, it can cause the electron to be emitted from the surface. This emitted electron is called a photoelectron.
How Photon Absorption Causes Photoelectron Emission
- A photon of frequency \( f \) has energy:
\( E = hf \)
- When this photon strikes an electron in a metal, the electron absorbs the energy in one single interaction.
- If the energy is:
- less than the work function → no electron is emitted.
- greater than or equal to the work function → an electron escapes the metal.
The work function \( \phi \) is the minimum energy needed to free an electron from the metal surface.
Condition for Photoelectron Emission
Photoelectron emission occurs only if:
\( hf \ge \phi \)
- If \( hf < \phi \) → no electrons are emitted, regardless of intensity.
- If \( hf = \phi \) → electron just escapes with zero kinetic energy.
- If \( hf > \phi \) → electron is emitted with kinetic energy.
Kinetic Energy of the Emitted Photoelectron
The maximum kinetic energy of emitted electrons is given by Einstein’s photoelectric equation:
- If photon energy increases → electrons are emitted with higher kinetic energy.
- Increasing intensity only increases the number of emitted electrons, not their energy.
Key Assumptions of the Photon Model
- A single photon interacts with a single electron (1:1 interaction).
- Absorption of a photon is instantaneous.
- Energy cannot accumulate from multiple low-energy photons.
Why Photon Absorption Causes Emission (Not Wave Energy)
- The wave model predicts that energy should build up gradually → but experiments show electrons are emitted instantly.
- Therefore, energy must come in discrete packets (photons), proving the quantum nature of light.
Example (Easy)
A photon of frequency \( f \) hits an electron, and the metal has work function \( \phi \). State the condition required for electron emission.
▶️ Answer / Explanation
Electron emission occurs only if \( hf \ge \phi \).
Example (Medium)
Why can increasing the intensity of light fail to eject electrons from a metal surface?
▶️ Answer / Explanation
- Intensity increases the number of photons per second.
- If frequency is below threshold (i.e., \( hf < \phi \)), each photon has insufficient energy.
- No electrons will be emitted regardless of intensity.
Example (Hard)
A metal has a work function of \( 3.0\times10^{-19}\ \mathrm{J} \). Light of frequency \( 1.0\times10^{15}\ \mathrm{Hz} \) shines on it. Find the maximum kinetic energy of the emitted electron.
▶️ Answer / Explanation
Step 1: Photon energy
\( E = hf = (6.63\times10^{-34})(1.0\times10^{15}) = 6.63\times10^{-19}\ \mathrm{J} \)
Step 2: Maximum KE
\( E_{\text{k(max)}} = hf – \phi \)
\( E_{\text{k(max)}} = 6.63\times10^{-19} – 3.0\times10^{-19} = 3.63\times10^{-19}\ \mathrm{J} \)
Maximum KE = \( 3.63\times10^{-19}\ \mathrm{J} \)
Threshold Frequency, Work Function and Einstein’s Photoelectric Equation
The photoelectric effect shows that electromagnetic radiation transfers energy in discrete packets called photons. For an electron to be emitted from a metal surface, a photon must supply enough energy to overcome the metal’s work function.
Work Function \( \phi \)
The work function \( \phi \) is the minimum energy required to remove an electron from the surface of a metal.
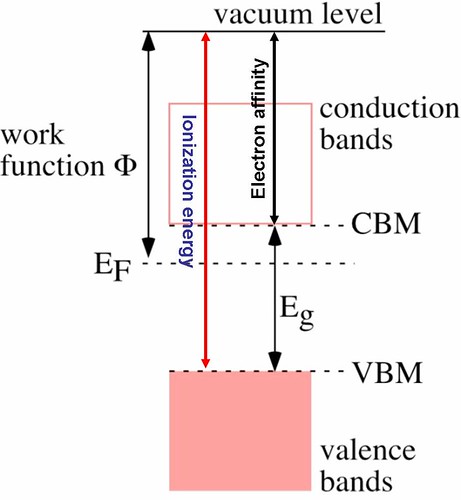
- Measured in joules (J) or electronvolts (eV).
- Different metals have different work functions.
- If the photon energy is less than \( \phi \), no electrons are emitted.
Condition for emission: \( hf \ge \phi \)
Threshold Frequency \( f_0 \)
The threshold frequency \( f_0 \) is the minimum frequency of incident radiation required to release electrons.
- If \( f < f_0 \) → no electrons emitted regardless of intensity.
- If \( f \ge f_0 \) → electrons are emitted.
The threshold frequency is related to work function by:
\( \phi = hf_0 \)
Einstein’s Photoelectric Equation
When a photon of frequency \( f \) strikes an electron:
- Photon energy = \( hf \)
- Energy needed to escape metal = \( \phi \)
- Remaining energy becomes the electron’s kinetic energy
The equation is:
\( hf = \phi + \dfrac{1}{2}mv_{\text{max}}^{2} \)
- \( m \) = electron mass
- \( v_{\text{max}} \) = maximum velocity of emitted electrons
- Only some electrons have maximum kinetic energy → others have less.
Meaning of the Equation
- If \( f = f_0 \) → electron leaves with zero kinetic energy.
- If \( f > f_0 \) → electron gains kinetic energy:
\( \dfrac{1}{2}mv_{\text{max}}^{2} = hf – \phi \)
- Increasing intensity increases number of electrons emitted, but does not increase their energy.
- Only increasing frequency increases the maximum kinetic energy.
Graphical Representation
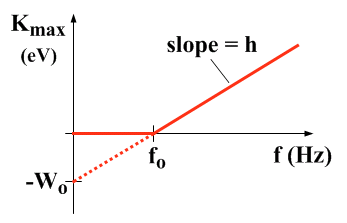
- A graph of \( KE_{\text{max}} \) vs \( f \) is a straight line:
- Gradient = \( h \)
- x-intercept = \( f_0 \)
- y-intercept = \( -\phi \)
Example (Easy)
A metal has work function \( \phi = 4.0\times10^{-19}\ \mathrm{J} \). Find its threshold frequency.
▶️ Answer / Explanation
\( f_0 = \dfrac{\phi}{h} = \dfrac{4.0\times10^{-19}}{6.63\times10^{-34}} = 6.03\times10^{14}\ \mathrm{Hz} \)
Example (Medium)
A photon of frequency \( 1.2\times10^{15}\ \mathrm{Hz} \) hits a metal with \( \phi = 5.5\times10^{-19}\ \mathrm{J} \). Find the maximum kinetic energy of the emitted electron.
▶️ Answer / Explanation
Photon energy:
\( hf = (6.63\times10^{-34})(1.2\times10^{15}) = 7.96\times10^{-19}\ \mathrm{J} \)
Maximum KE:
\( KE_{\text{max}} = hf – \phi = 7.96\times10^{-19} – 5.5\times10^{-19} = 2.46\times10^{-19}\ \mathrm{J} \)
Example (Hard)
Light of frequency \( 8.0\times10^{14}\ \mathrm{Hz} \) shines on a metal with \( \phi = 3.5\times10^{-19}\ \mathrm{J} \). Calculate the maximum speed of the emitted electron.
▶️ Answer / Explanation
Step 1: Photon energy
\( hf = (6.63\times10^{-34})(8.0\times10^{14}) = 5.30\times10^{-19}\ \mathrm{J} \)
Step 2: Maximum kinetic energy
\( KE_{\text{max}} = hf – \phi = 5.30\times10^{-19} – 3.5\times10^{-19} = 1.80\times10^{-19}\ \mathrm{J} \)
Step 3: Use \( \dfrac{1}{2}mv^{2} = KE_{\text{max}} \)
\( v = \sqrt{\dfrac{2(1.80\times10^{-19})}{9.11\times10^{-31}}} = 6.29\times10^{5}\ \mathrm{m\,s^{-1}} \)
Maximum speed = \( 6.3\times10^{5}\ \mathrm{m\,s^{-1}} \)