Edexcel A Level (IAL) Physics-2.31 Atomic Line Spectra- Study Notes- New Syllabus

Atomic Line Spectra and Energy Level Transitions

Atoms contain electrons that can only occupy specific, fixed (discrete) energy levels. These energy levels are quantised, meaning electrons cannot have energies between them.

When electrons move between these energy levels, they emit or absorb photons. This produces the characteristic atomic line spectra.

 Discrete Energy Levels

• Electrons occupy fixed energy levels (e.g., \( E_1, E_2, E_3, \ldots \)).
• Each level has a specific energy measured in joules (J) or electronvolts (eV).
• The lowest energy level is called the ground state.
• Higher levels are excited states.

Electrons can transition only between these discrete levels → producing photons of fixed frequency.

Emission of Radiation

When an electron falls from a higher level \( E_{\text{high}} \) to a lower level \( E_{\text{low}} \):

• Energy is released.
• A photon is emitted.
• The photon’s energy equals the difference between the two levels.

\( hf = E_{\text{high}} – E_{\text{low}} \)

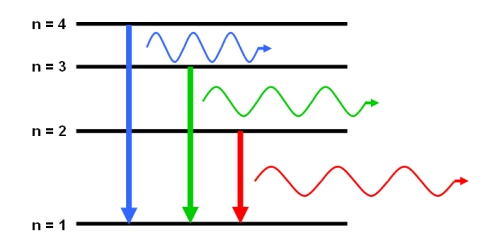
These emitted photons form the emission line spectrum of the atom.

Absorption of Radiation

When a photon with the correct energy hits an atom, an electron can absorb it and move to a higher energy level: 

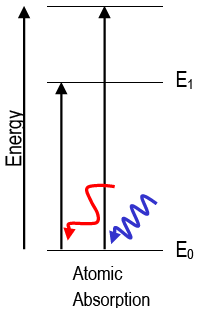
\( hf = E_{\text{high}} – E_{\text{low}} \)

This forms the absorption line spectrum — dark lines at specific frequencies (or wavelengths).

Calculating the Frequency of Emitted or Absorbed Radiation

Use the photon energy relationship:

\( E_{\text{photon}} = hf \)

And since the energy comes from the difference between levels:

\( hf = \Delta E = E_{\text{high}} – E_{\text{low}} \)

Thus:

\( f = \dfrac{\Delta E}{h} \)

You may also calculate wavelength using:

\( c = f\lambda \qquad \Rightarrow \qquad \lambda = \dfrac{c}{f} \)

Why Line Spectra Occur

• Only specific energy differences are allowed → only certain frequencies are emitted/absorbed.
• This creates distinct bright or dark lines.
• Each element has a unique set of energy levels → a unique spectrum.

 Emission vs Absorption Spectra

• Emission spectrum: bright coloured lines on a dark background.
• Absorption spectrum: dark lines on a continuous spectrum.
• Both correspond to the same energy differences between levels.