Edexcel A Level (IAL) Physics-2.35 - 2.36 Charge and Energy Conservation in Circuits- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -2.35 – 2.36 Charge and Energy Conservation in Circuits- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -2.35 – 2.36 Charge and Energy Conservation in Circuits- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
Current Distribution in Circuits and Charge Conservation
Electric current is the flow of electric charge around a circuit. The way current divides and behaves in a circuit is governed by the fundamental principle of charge conservation.
Charge conservation: Charge cannot be created or destroyed — it can only move from one place to another.
Charge Conservation and Current
Since electric current is defined as:
\( I = \dfrac{\Delta Q}{\Delta t} \)
- Current represents how fast charge flows.
- If charge is conserved, then current must also be conserved at any junction.
Meaning: Whatever charge flows into a point must flow out of it.
Current at a Junction (Kirchhoff’s First Law)
At any junction in a circuit:
\( I_{\text{in}} = I_{\text{out}} \)
This is a direct consequence of charge conservation.
- If 5 A flows into a junction and splits into two branches:
- The currents in the two branches must add up to 5 A.
- No charge can accumulate at the junction.
Current in Series Circuits
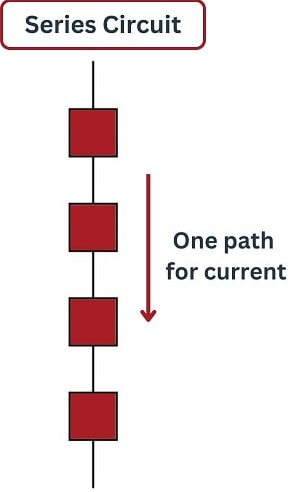
- All components share the same current.
- Because there is only one path for charge flow.
- Charge per second must be the same everywhere in the loop.
Thus, in series:
\( I_1 = I_2 = I_3 = \ldots \)
Current in Parallel Circuits
- Total current entering the parallel section equals the sum of currents in each branch.
- More paths → charge splits depending on resistance.
\( I_{\text{total}} = I_1 + I_2 + I_3 + \ldots \)
This ensures that no charge builds up or disappears — charge conservation holds.
Why Charge Cannot Accumulate
- If charge accumulated, the junction would develop a huge electric field.
- This would instantly push charge away.
- Therefore, circuits naturally enforce \( I_{\text{in}} = I_{\text{out}} \).
Relationship to Electron Flow
- In metals, electrons move but the total number of electrons is constant → conserved.
- Current is steady because electrons do not pile up anywhere.
- A steady current means equal flow rates into and out of every point.
Example (Easy)
3 A of current enters a junction. Two wires leave carrying 1 A and \( I \) A. Find \( I \).
▶️ Answer / Explanation
Using charge conservation:
\( I_{\text{in}} = I_{\text{out}} \)
\( 3 = 1 + I \)
\( I = 2\ \mathrm{A} \)
Example (Medium)
In a parallel circuit, the total current is \( 0.8\ \mathrm{A} \). The current in branch 1 is \( 0.3\ \mathrm{A} \) and in branch 2 is \( 0.4\ \mathrm{A} \). Does this obey charge conservation?
▶️ Answer / Explanation
\( I_{\text{total}} = 0.8\ \mathrm{A} \)
\( I_1 + I_2 = 0.3 + 0.4 = 0.7\ \mathrm{A} \)
Since \( 0.7 \ne 0.8 \), charge conservation is not satisfied.
There must be another branch or measurement error.
Example (Hard)
A circuit has three branches carrying \( 1.2\ \mathrm{A} \), \( 0.5\ \mathrm{A} \), and \( 0.9\ \mathrm{A} \). These combine at a junction into a single wire. Find the current in the final wire and explain using charge conservation.
▶️ Answer / Explanation
Total outgoing current:
\( I = 1.2 + 0.5 + 0.9 = 2.6\ \mathrm{A} \)
Explanation:
- All the charge from the three branches enters the final wire.
- No charge is lost or stored at the junction.
- Therefore, the current must add to \( 2.6\ \mathrm{A} \).
Distribution of Potential Differences in a Circuit and Energy Conservation
The way potential differences (voltages) are shared in a circuit is governed by the fundamental principle of energy conservation. Voltage tells us how much energy each coulomb of charge gains or loses as it moves through a component.
Energy Conservation in Electrical Circuits
As charge moves around a circuit:
- The battery provides energy to each coulomb of charge.
- Components like resistors, lamps or motors use up energy from the charge.
- Total energy supplied per coulomb = total energy used per coulomb.
This leads directly to the conservation rule for potential differences.
Definition of Potential Difference
Potential difference is energy transferred per unit charge:
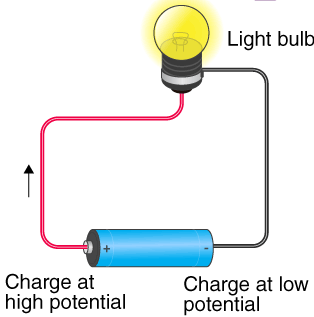
\( V = \dfrac{W}{Q} \)
- A 9 V battery gives \( 9\ \mathrm{J} \) of energy to every coulomb.
- A 6 V resistor removes \( 6\ \mathrm{J} \) of energy from every coulomb.
Distribution of Voltage in a Series Circuit
- Charge passes through each component in turn.
- Each component takes some energy from the charge.
- The sum of the voltages across all components equals the supply voltage.
\( V_{\text{supply}} = V_1 + V_2 + V_3 + \ldots \)
Why? Because the total energy gained from the battery must equal the total energy lost in the circuit.
Distribution of Voltage in a Parallel Circuit
- Each branch connects directly across the supply.
- Each branch receives the same energy per coulomb.
\( V_{\text{branch 1}} = V_{\text{branch 2}} = V_{\text{supply}} \)
Reason: Since the start and end of each branch are connected directly to the same two points, each coulomb gains and loses the same energy.
Energy Changes Around a Complete Loop
For any complete loop in a circuit:
\( \sum V_{\text{gains}} = \sum V_{\text{losses}} \)
- Batteries give energy → positive voltage gain.
- Resistors, bulbs, motors use energy → voltage drops.
Energy in = Energy out → Voltage in = Voltage out
Real Meaning of “Voltage Drop”
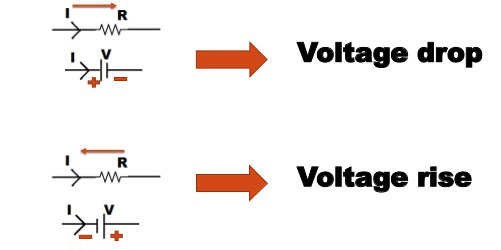
- A resistor converts electrical energy into heat.
- A lamp converts electrical energy to light and heat.
- This energy loss per coulomb appears as a “voltage drop”.
Example (Easy)
A 9 V battery is connected to two resistors in series. One resistor has a 4 V drop. What is the voltage across the second resistor?
▶️ Answer / Explanation
Use energy conservation:
\( 9 = 4 + V_2 \)
\( V_2 = 5\ \mathrm{V} \)
Total drop equals total supply.
Example (Medium)
A lamp and a motor are connected in series to a 12 V supply. If the lamp takes 7 V, how much energy does each coulomb lose in the motor?
▶️ Answer / Explanation
Voltage drop = energy per coulomb
Voltage across motor:
\( 12 – 7 = 5\ \mathrm{V} \)
Energy lost per coulomb = 5 J
Example (Hard)
Three components in series have voltage drops of \( V_1 \), \( V_2 \), and \( V_3 \). The supply is 18 V. If \( V_1 = 5\ \mathrm{V} \) and \( V_2 = 6.5\ \mathrm{V} \), calculate \( V_3 \) and explain using energy conservation.
▶️ Answer / Explanation
Total voltage drop must equal supply:
\( V_3 = 18 – (5 + 6.5) \)
\( V_3 = 6.5\ \mathrm{V} \)
Explanation:
- The battery gives 18 J to each coulomb.
- The drops 5 J + 6.5 J + 6.5 J = 18 J account for all the energy.
- Energy is conserved around the loop.