Edexcel A Level (IAL) Physics-2.37 Resistance in Series & Parallel- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -2.37 Resistance in Series & Parallel- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -2.37 Resistance in Series & Parallel- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
- be able to derive the equations for combining resistances in series and parallel using the principles of charge and energy conservation, and be able to use these equations
Combining Resistances in Series and Parallel
Resistors can be connected in series or parallel. Using the principles of charge conservation and energy conservation, we can derive formulas for their equivalent resistance.
Resistors in Series
When resistors are in series:
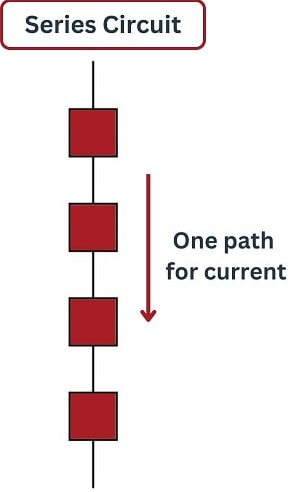
- The same current flows through each resistor (charge conservation).
- The total potential difference across the combination is the sum of individual drops (energy conservation).
Voltage rule:
\( V_{\text{total}} = V_1 + V_2 + V_3 + \ldots \)![]()
Using \( V = IR \):
- Let the current through each resistor be \( I \).
- Then: \( V_1 = IR_1 \), \( V_2 = IR_2 \), etc.
Thus:
\( V_{\text{total}} = I(R_1 + R_2 + R_3 + \ldots) \)
But also:
\( V_{\text{total}} = IR_{\text{eq}} \)
Therefore:
\( R_{\text{eq}} = R_1 + R_2 + R_3 + \ldots \)
Resistors in Parallel
When resistors are in parallel:

- The potential difference across each branch is the same (energy conservation).
- The total current is the sum of branch currents (charge conservation).
Voltage rule:
\( V = V_1 = V_2 = V_3 = \ldots \)![]()
Current rule:
\( I_{\text{total}} = I_1 + I_2 + I_3 + \ldots \)
Using \( I = \dfrac{V}{R} \), branch currents are:
\( I_1 = \dfrac{V}{R_1}, \quad I_2 = \dfrac{V}{R_2}, \quad I_3 = \dfrac{V}{R_3}, \ldots \)
Thus:
\( I_{\text{total}} = V\left( \dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3} + \ldots \right) \)
But by definition:
\( I_{\text{total}} = \dfrac{V}{R_{\text{eq}}} \)
So:
\( \dfrac{V}{R_{\text{eq}}} = V\left( \dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3} + \ldots \right) \)
Cancel \( V \):
\( \dfrac{1}{R_{\text{eq}}} = \dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3} + \ldots \)
Summary Table
| Connection | Voltage Rule | Current Rule | Equivalent Resistance |
|---|---|---|---|
| Series | \( V_{\text{total}} = V_1 + V_2 + \ldots \) | \( I_1 = I_2 = \ldots \) | \( R_{\text{eq}} = R_1 + R_2 + \ldots \) |
| Parallel | \( V_1 = V_2 = \ldots = V \) | \( I_{\text{total}} = I_1 + I_2 + \ldots \) | \( \dfrac{1}{R_{\text{eq}}} = \dfrac{1}{R_1} + \dfrac{1}{R_2} + \ldots \) |
Example (Easy)
Find the equivalent resistance of two resistors in series: \( 4\ \Omega \) and \( 6\ \Omega \).
▶️ Answer / Explanation
\( R_{\text{eq}} = 4 + 6 = 10\ \Omega \)
Example (Medium)
Calculate the equivalent resistance of two resistors in parallel: \( 8\ \Omega \) and \( 12\ \Omega \).
▶️ Answer / Explanation
\( \dfrac{1}{R_{\text{eq}}} = \dfrac{1}{8} + \dfrac{1}{12} \)
\( \dfrac{1}{R_{\text{eq}}} = \dfrac{3}{24} + \dfrac{2}{24} = \dfrac{5}{24} \)
\( R_{\text{eq}} = \dfrac{24}{5} = 4.8\ \Omega \)
Example (Hard)
Two resistors of \( 10\ \Omega \) and \( R \) are connected in parallel. Their equivalent resistance is \( 4\ \Omega \). Find the value of \( R \).
▶️ Answer / Explanation
\( \dfrac{1}{4} = \dfrac{1}{10} + \dfrac{1}{R} \)
\( \dfrac{1}{R} = \dfrac{1}{4} – \dfrac{1}{10} = \dfrac{5 – 2}{20} = \dfrac{3}{20} \)
\( R = \dfrac{20}{3} = 6.67\ \Omega \)
