Edexcel A Level (IAL) Physics-2.40 Electrical Resistivity- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -2.40 Electrical Resistivity- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -2.40 Electrical Resistivity- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
- be able to use the equation \(R=\dfrac{\rho l}{A}\)
Resistance of a Wire \( R = \rho \dfrac{l}{A} \)
The resistance of a conductor depends not only on the material but also on its dimensions. The equation \( R = \rho\dfrac{l}{A} \) relates resistance to the wire’s length and cross-sectional area through a material constant called resistivity.
Definition of Resistivity
Resistivity \( \rho \) is a property of the material that tells us how strongly it opposes current flow.

- \( \rho \) = resistivity (ohm metre, \( \Omega\,\mathrm{m} \))
- Low \( \rho \): good conductors (copper, silver)
- High \( \rho \): poor conductors/insulators
Resistivity depends on material and temperature.
Resistance of a Wire
The resistance of a uniform conductor is given by:
![]()
\( R = \rho \dfrac{l}{A} \)
- \( R \) = resistance (ohms, \( \Omega \))
- \( l \) = length of wire (m)
- \( A \) = cross-sectional area (m²)
- \( \rho \) = resistivity (Ωm)
Physical Meaning
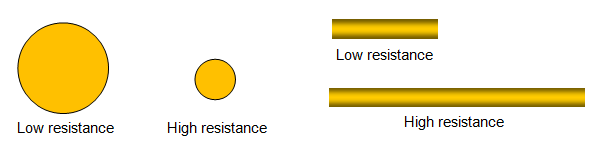
- Longer wire → charges travel further → more collisions → higher resistance.
- Thicker wire (larger area) → more paths for electrons → lower resistance.
- Material with higher \( \rho \) → greater opposition to current.
Rearranged Forms
\( \rho = R \dfrac{A}{l} \)
\( A = \rho \dfrac{l}{R} \)
Cross-Sectional Area for Circular Wires
If the wire has diameter \( d \):
\( A = \dfrac{\pi d^{2}}{4} \)
Always remember to convert diameter → radius → metres.
Example (Easy)
A copper wire of length \( 2\ \mathrm{m} \) and area \( 1.5\times10^{-6}\ \mathrm{m^{2}} \) has resistivity \( 1.7\times10^{-8}\ \Omega\mathrm{m} \). Find its resistance.
▶️ Answer / Explanation
\( R = \rho\dfrac{l}{A} = (1.7\times10^{-8}) \dfrac{2}{1.5\times10^{-6}} \)
\( R = 2.27\times10^{-2}\ \Omega \)
Example (Medium)
A wire is \( 5\ \mathrm{m} \) long and has resistance \( 4\ \Omega \). If the cross-sectional area is \( 2.0\times10^{-7}\ \mathrm{m^{2}} \), find the resistivity.
▶️ Answer / Explanation
\( \rho = R \dfrac{A}{l} = 4 \cdot \dfrac{2.0\times10^{-7}}{5} \)
\( \rho = 1.6\times10^{-7}\ \Omega\mathrm{m} \)
Example (Hard)
A wire of resistivity \( 4.0\times10^{-7}\ \Omega\mathrm{m} \) is \( 12\ \mathrm{m} \) long and has resistance \( 3\ \Omega \). Find its diameter.
▶️ Answer / Explanation
Step 1: Find area.
\( A = \rho\dfrac{l}{R} = (4.0\times10^{-7})\dfrac{12}{3} = 1.6\times10^{-6}\ \mathrm{m^{2}} \)
Step 2: Use circular area formula.
\( A = \dfrac{\pi d^{2}}{4} \Rightarrow d = \sqrt{\dfrac{4A}{\pi}} \)
\( d = \sqrt{\dfrac{4(1.6\times10^{-6})}{\pi}} = 1.43\times10^{-3}\ \mathrm{m} \)
Diameter ≈ \( 1.43\ \mathrm{mm} \)
