Edexcel A Level (IAL) Physics-2.43 Potential Difference & Conductor Length- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -2.43 Potential Difference & Conductor Length- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -2.43 Potential Difference & Conductor Length- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
Potential Variation Along a Uniform Current-Carrying Wire
When a steady current flows through a uniform wire (constant cross-sectional area and constant resistivity), the potential difference across the wire drops uniformly with distance. This means the electric potential along the wire decreases linearly from one end to the other.
Why Potential Drops Along a Wire
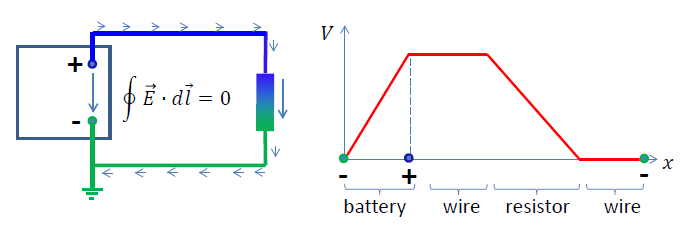
- A wire has resistance \( R \).
- When current \( I \) flows, energy is lost per unit length due to collisions of electrons with ions.
- This energy loss corresponds to a drop in potential.
- If the wire is uniform, each small segment behaves the same → same voltage drop per unit length.
Therefore, potential decreases at a constant rate along the wire.
The Linear Relationship
If the total potential difference across a wire of length \( L \) is \( V \), then the potential at a point a distance \( x \) from one end is:
\( V(x) = V \left( 1 – \dfrac{x}{L} \right) \)
This shows a straight-line decrease from full voltage at \( x = 0 \) to zero at \( x = L \) (if referenced to the negative terminal).
Constant Potential Gradient
For a uniform wire:
\( \text{Potential gradient} = \dfrac{V}{L} \ \text{(volts per metre)} \)
This is constant for all positions along the wire.
Meaning:
- Every 1 cm of wire drops the same amount of voltage.
- Halving the length → halves the potential difference.
- Doubling the length → doubles the potential difference (for same current).
Connection to Resistance
Total resistance of wire:
\( R = \rho \dfrac{L}{A} \)
Resistance per unit length:
\( \dfrac{R}{L} = \rho \dfrac{1}{A} \)
Thus potential drop per unit length is:
\( \dfrac{V}{L} = I \left( \dfrac{R}{L} \right) = I \rho \dfrac{1}{A} \)
This stays constant when \( \rho \), \( A \), and \( I \) are constant → linear decrease.
Applications
- Potentiometers use the linear drop in voltage to measure unknown voltages.
- Voltage dividers rely on predictable potential variation along resistive wires.
- Probes placed along the wire measure potential at different points (used in many practicals).
Example (Easy)
A uniform wire of length \( 1.0\ \mathrm{m} \) has a voltage of \( 6.0\ \mathrm{V} \) across it. What is the voltage drop per centimetre?
▶️ Answer / Explanation
Total drop = \( 6.0\ \mathrm{V} \)
Length = \( 100\ \mathrm{cm} \)
Drop per cm = \( \dfrac{6.0}{100} = 0.06\ \mathrm{V/cm} \)
Example (Medium)
A uniform wire is \( 80\ \mathrm{cm} \) long and has a total voltage of \( 5.0\ \mathrm{V} \) across it. What is the potential at a point \( 30\ \mathrm{cm} \) from one end?
▶️ Answer / Explanation
Use linear relation:
\( V(x) = V \left( 1 – \dfrac{x}{L} \right) \)
\( V(30) = 5.0 \left( 1 – \dfrac{30}{80} \right) \)
\( V(30) = 5.0 \left( 1 – 0.375 \right) = 5.0(0.625) = 3.125\ \mathrm{V} \)
Example (Hard)
A wire of resistivity \( 2.0\times10^{-7}\ \Omega\mathrm{m} \), cross-sectional area \( 1.0\times10^{-6}\ \mathrm{m^{2}} \), and length \( 2.0\ \mathrm{m} \) carries a current of \( 1.5\ \mathrm{A} \). Calculate the potential at a point \( 0.50\ \mathrm{m} \) from the negative terminal.
▶️ Answer / Explanation
Step 1: Find total resistance.
\( R = \rho\dfrac{L}{A} = (2.0\times10^{-7})\dfrac{2.0}{1.0\times10^{-6}} = 0.40\ \Omega \)
Step 2: Voltage across wire.
\( V = IR = 1.5 \times 0.40 = 0.60\ \mathrm{V} \)
Step 3: Use linear formula.
\( V(x) = V\left(1 – \dfrac{x}{L}\right) = 0.60 \left( 1 – \dfrac{0.50}{2.0} \right) \)
\( V(x) = 0.60 (0.75) = 0.45\ \mathrm{V} \)