Edexcel A Level (IAL) Physics-2.46 Electromotive Force- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -2.46 Electromotive Force- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -2.46 Electromotive Force- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
- know the definition of electromotive force (e.m.f.) and understand what is meant by internal resistance and know how to distinguish between e.m.f. and terminal potential difference
Electromotive Force (e.m.f.), Internal Resistance and Terminal Potential Difference
Cells and power supplies provide energy to a circuit, but real sources are not ideal. They have an internal resistance that affects the voltage delivered to the external load.
Electromotive Force (e.m.f.) — Definition
The e.m.f. \( \mathcal{E} \) of a source is the energy supplied per unit charge by the source when no current is flowing.
![]()
\( \mathcal{E} = \dfrac{W}{Q} \)
- Units: volts (V)
- It is the maximum possible voltage the cell can supply.
- Measured when the circuit is open (no current drawn).
Internal Resistance \( r \)
Every cell or power supply has some resistance inside it due to its construction. This is called internal resistance.
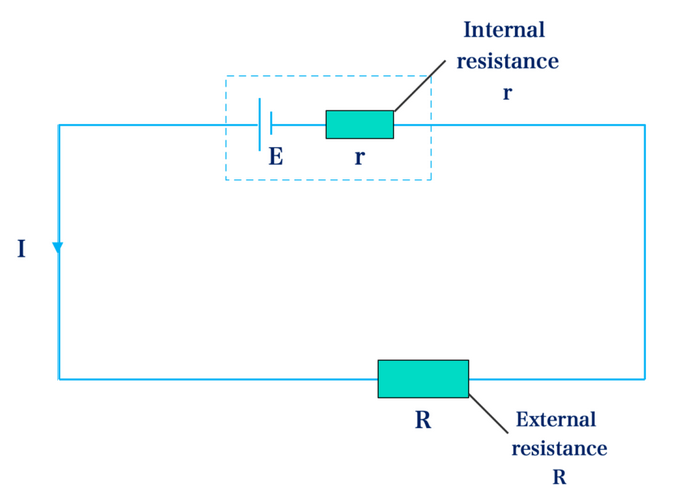
- Causes a voltage drop inside the cell.
- Energy is lost as heat inside the cell.
- Reduces the terminal voltage when current flows.
Voltage lost inside cell:
\( V_{\text{lost}} = Ir \)
Terminal Potential Difference (t.p.d.)
The terminal potential difference \( V \) is the voltage available across the external circuit when current is flowing.![]()
![]()
\( V = \mathcal{E} – Ir \)
Thus:
- Terminal p.d. is always less than the e.m.f. when current flows.
- The greater the current, the larger the internal voltage loss \( Ir \), and the smaller the t.p.d.
- If no current flows (\( I = 0 \)) → \( V = \mathcal{E} \).
Distinguishing e.m.f. and Terminal p.d.
![]()
| Quantity | Definition | When measured |
|---|---|---|
| e.m.f. \( \mathcal{E} \) | Energy provided per unit charge by the source | When no current flows (open circuit) |
| Terminal p.d. \( V \) | Voltage across external load while current flows | When circuit delivers power to a load |
Circuit Equation Including Internal Resistance
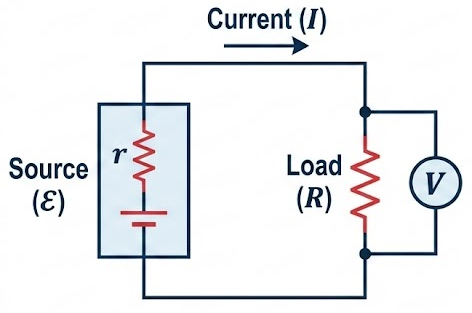
For a source with internal resistance \( r \) and external load \( R \):
\( \mathcal{E} = V + Ir \)
And since \( V = IR \):
\( \mathcal{E} = IR + Ir = I(R + r) \)
Using Graphs to Determine \( r \) and \( \mathcal{E} \)
Plot terminal voltage \( V \) against current \( I \):
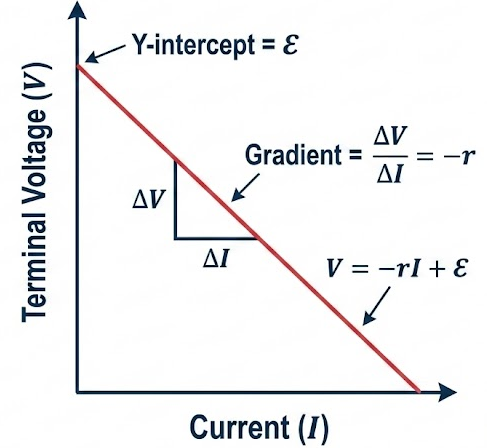
- Straight line of form \( V = -rI + \mathcal{E} \)
- Gradient = \( -r \)
- Y-intercept = \( \mathcal{E} \)
Example (Easy)
A cell has an e.m.f. of \( 6.0\ \mathrm{V} \) and no current is drawn from it. What is its terminal p.d.?
▶️ Answer / Explanation
No current → \( I = 0 \)
\( V = \mathcal{E} – Ir = 6.0 – 0 = 6.0\ \mathrm{V} \)
Example (Medium)
A 12 V battery has internal resistance \( 0.40\ \Omega \). If it supplies \( 3.0\ \mathrm{A} \), calculate the terminal p.d.
▶️ Answer / Explanation
\( V = \mathcal{E} – Ir = 12 – (3.0)(0.40) = 12 – 1.2 = 10.8\ \mathrm{V} \)
Example (Hard)
A cell has e.m.f. \( 9.0\ \mathrm{V} \) and internal resistance \( 0.50\ \Omega \). It is connected to an external resistor \( R \), and the terminal voltage is measured to be \( 6.0\ \mathrm{V} \). Find the current and the value of \( R \).
▶️ Answer / Explanation
Step 1: Find current.
\( V = \mathcal{E} – Ir \)
\( 6.0 = 9.0 – 0.50I \)
\( 0.50I = 3.0 \Rightarrow I = 6.0\ \mathrm{A} \)
Step 2: Find external resistance.
\( V = IR \Rightarrow R = \dfrac{6.0}{6.0} = 1.0\ \Omega \)
