Edexcel A Level (IAL) Physics-2.49 Core Practical 8: Investigating E.M.F & Internal Resistance- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -2.49 Core Practical 8: Investigating E.M.F & Internal Resistance- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -2.49 Core Practical 8: Investigating E.M.F & Internal Resistance- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
CORE PRACTICAL 8: Determine the e.m.f. and Internal Resistance of an Electrical Cell
This practical determines both the e.m.f. \( \mathcal{E} \) and internal resistance \( r \) of a cell by measuring how the terminal voltage varies with current.
The key equation used is:
\( V = \mathcal{E} – Ir \)
Apparatus
- Cell or battery
- Variable resistor (rheostat) or selection of resistors
- Ammeter (A) — in series
- Voltmeter (V) — across the cell (parallel)
- Switch
- Connecting leads
Circuit Diagram
Method
- Set up the circuit with the variable resistor at its maximum resistance (to minimise current initially).
- Close the switch and record:
- Current \( I \)
- Terminal voltage \( V \)
- Vary the resistance to obtain a wide range of currents (e.g., 0.1 A – 1.0 A), each time recording the corresponding voltage.
- Open the switch between readings to minimise heating in the cell (heating changes internal resistance).
- Plot a graph of terminal voltage \( V \) (y-axis) against current \( I \) (x-axis).
- Add a best-fit straight line through the points.
How to Determine e.m.f. and Internal Resistance
The equation:
\( V = \mathcal{E} – Ir \)
is of the form:
\( y = c + mx \)
with:
- Dependent variable: \( V \)
- Independent variable: \( I \)
- Gradient: \( -r \)
- Y-intercept: \( \mathcal{E} \)
Thus:
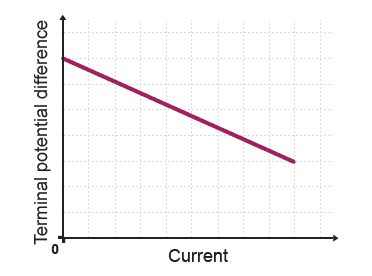
- E.m.f. = y-intercept of the line
- Internal resistance = negative gradient of the line
Why This Method Works
- As current increases, more energy is lost in the internal resistance.
- This causes terminal voltage to drop linearly with current.
- Measuring the rate of this drop reveals \( r \), while the intercept gives \( \mathcal{E} \).
Safety Considerations
- Do not short-circuit the cell (very large currents can cause heating).
- Use low currents for brief periods only.
- Open the switch between readings to limit heating of wires and cell.
Sources of Error & Improvements
- Heating of cell: use low currents; open switch between readings.
- Ammeter/voltmeter errors: use digital meters for higher precision.
- Poor contact resistance: ensure all connections are tight.
- Graph errors: take at least 6 readings across a wide current range.
Example Data & Calculation
Measured values:
| Current \( I \) (A) | Voltage \( V \) (V) |
|---|---|
| 0.2 | 1.45 |
| 0.4 | 1.32 |
| 0.6 | 1.19 |
| 0.8 | 1.05 |
| 1.0 | 0.92 |
▶️ Answer / Interpretation
Step 1: Plot V against I Graph is a straight descending line.
Step 2: Find y-intercept
Intercept ≈ \( 1.58\ \mathrm{V} \) → this is \( \mathcal{E} \)
Step 3: Find gradient
Between (0.2, 1.45) and (1.0, 0.92):
\( \text{gradient} = \dfrac{0.92 – 1.45}{1.0 – 0.2} = \dfrac{-0.53}{0.8} = -0.66\ \Omega \)
Internal resistance: \( r = 0.66\ \Omega \).
Conclusion
- The e.m.f. of the cell is found from the intercept of the V–I graph.
- The internal resistance is found from the magnitude of the negative gradient.
- This is a reliable, standard method used in all physics laboratories.