Edexcel A Level (IAL) Physics-2.9 Stationary Waves- Study Notes- New Syllabus

Standing (Stationary) Waves: Formation, Nodes, and Antinodes

A standing or stationary wave is a wave pattern that does not travel through the medium. Instead, the wave appears to oscillate in place with fixed points of no movement (nodes) and points of maximum movement (antinodes).

 What is a Standing Wave?

A standing wave is formed when two coherent waves of the same:

• frequency
• wavelength
• amplitude
• speed

travel in opposite directions and superpose.

No net transfer of energy occurs along a standing wave.

How a Standing Wave is Formed

• A wave reflects from a boundary (e.g., fixed end of a string).
• The reflected wave travels back and overlaps with the incoming wave.
• Superposition causes:
  • constructive interference at antinodes
  • destructive interference at nodes
• This creates a stable pattern of nodes and antinodes.

Key condition: Standing waves occur only at resonant frequencies of the medium (e.g., allowed harmonics on a string or air column).

Nodes and Antinodes

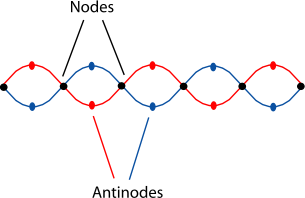
• Node (N):
  • Point of zero displacement (always stationary).
  • Caused by complete destructive interference.
  • Nodes occur at fixed positions, spacing = \( \lambda/2 \) apart.
• Antinode (A):
  • Point of maximum displacement.
  • Caused by constructive interference.
  • Antinodes also occur \( \lambda/2 \) apart.
  • Distance between a node and adjacent antinode = \( \lambda/4 \).

Features of Standing Waves

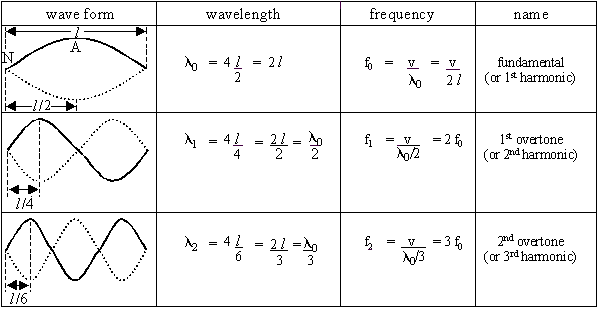
• Energy is stored locally, not transmitted.
• Occurs in strings, air columns, microwaves, sound tubes.
• Forms patterns corresponding to harmonics:
  • First harmonic (fundamental)
  • Second harmonic
  • Third harmonic
  • etc.

Identifying Nodes and Antinodes

• Nodes → points that do not move during oscillation.
• Antinodes → points that move with maximum amplitude.
• On a snapshot graph: nodes are points on the horizontal axis.
• On a time graph: nodes have zero displacement at all times.