Edexcel A Level (IAL) Physics-4.12 - 4.13 Defining an Electric Field & Electric Field Strength- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -4.12 – 4.13 Defining an Electric Field & Electric Field Strength- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -4.12 – 4.13 Defining an Electric Field & Electric Field Strength- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
- understand that an electric field (force field) is defined as a region where a charged particle experiences a force
- understand that electric field strength is defined as E = F/Q and be able to use this equation
Electric Field (Force Field)
An electric field is a type of force field. It describes the region of space in which an electric charge experiences a force due to the presence of other charges.
Definition of an Electric Field
Electric field: A region of space where a charged particle experiences an electric force.
![]()
This means:
- If a charged particle is placed in an electric field, it will experience a force.
- If no charged particle is present, the field still exists.
- The field represents the influence of charges at a distance.
Electric Field as a Force Field
An electric field is called a force field because:
- It assigns a force to every charged particle placed in the region.
- The force depends on the charge of the particle.
- The force acts without physical contact.
Other examples of force fields include:
- Gravitational fields (act on mass)
- Magnetic fields (act on moving charges)
Direction of an Electric Field
The direction of an electric field at a point is defined as:
![]()
The direction of the force acting on a positive test charge placed at that point.
- Positive charges experience force in the direction of the field.
- Negative charges experience force opposite to the field direction.
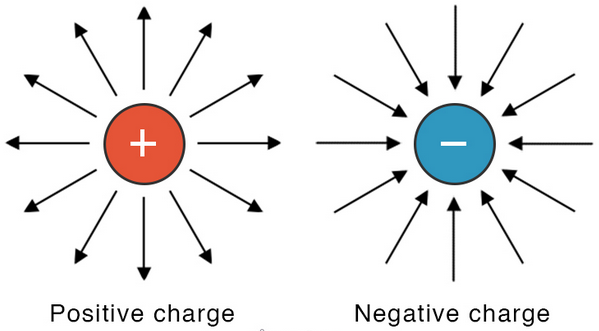
Source of Electric Fields
- Electric fields are produced by electric charges.
- A positive charge produces an outward electric field.
- A negative charge produces an inward electric field.
The field exists even if no other charges are present.
Physical Meaning
- The electric field allows forces to be explained as interactions through space.
- It avoids the idea of “action at a distance”.
- Energy is stored in the electric field.
Example (Easy)
What happens if a positive charge is placed in an electric field?
▶️ Answer / Explanation
- The charge experiences a force.
- The force acts in the direction of the electric field.
Example (Medium)
Why does a negative charge move opposite to the direction of the electric field?
▶️ Answer / Explanation
- The electric field direction is defined using a positive test charge.
- A negative charge experiences a force in the opposite direction.
Example (Hard)
Explain why an electric field can exist in empty space.
▶️ Answer / Explanation
- The field is created by charges.
- It represents the ability to exert a force.
- A test charge is not required for the field to exist.
Electric Field Strength \( E = \dfrac{F}{Q} \)
Electric field strength describes how strong an electric field is at a particular point. It tells us how much force a charged particle would experience per unit charge.
Definition of Electric Field Strength
Electric field strength at a point is defined as the force per unit positive charge acting at that point.![]()
\( E = \dfrac{F}{Q} \)
- \( E \) = electric field strength (N C⁻¹)
- \( F \) = electric force on the charge (N)
- \( Q \) = charge experiencing the force (C)
Meaning of the Definition
- Electric field strength depends on the field, not on the test charge.
- A stronger field produces a larger force on a given charge.
- The definition uses a positive test charge.
Rearranging the equation:
\( F = EQ \)
This form is often used to calculate the force on a charged particle in an electric field.
Direction of Electric Field Strength
- The direction of \( E \) is the direction of the force on a positive charge.
- A negative charge experiences a force opposite to the direction of \( E \).
Units of Electric Field Strength
- Unit: newton per coulomb (N C⁻¹)
- Equivalent unit: volt per metre (V m⁻¹) (covered later)
Applying the Equation \( E = \dfrac{F}{Q} \)
- Find field strength if force and charge are known.
- Find force on a charge if field strength is known.
- Works for uniform and non-uniform electric fields.
Example (Easy)
A force of \( 4.0\times10^{-6}\ \mathrm{N} \) acts on a charge of \( 2.0\times10^{-6}\ \mathrm{C} \). Calculate the electric field strength.
▶️ Answer / Explanation
\( E = \dfrac{F}{Q} = \dfrac{4.0\times10^{-6}}{2.0\times10^{-6}} = 2.0\ \mathrm{N\,C^{-1}} \)
Example (Medium)
An electric field has strength \( 500\ \mathrm{N\,C^{-1}} \). Find the force acting on a charge of \( 3.0\times10^{-6}\ \mathrm{C} \).
▶️ Answer / Explanation
\( F = EQ = 500 \times 3.0\times10^{-6} = 1.5\times10^{-3}\ \mathrm{N} \)
Example (Hard)
A negative charge of \( 4.0\times10^{-6}\ \mathrm{C} \) is placed in a uniform electric field of strength \( 250\ \mathrm{N\,C^{-1}} \). Determine the magnitude and direction of the force on the charge.
▶️ Answer / Explanation
Magnitude:
\( F = EQ = 250 \times 4.0\times10^{-6} = 1.0\times10^{-3}\ \mathrm{N} \)
Direction:
- Field direction is defined for a positive charge.
- The charge is negative.
- Force acts opposite to the electric field direction.
