Edexcel A Level (IAL) Physics-4.18 - 4.19 Electric Potential for a Radial Field & Uniform Electric Fields- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -4.18 – 4.19 Electric Potential for a Radial Field & Uniform Electric Fields- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -4.18 – 4.19 Electric Potential for a Radial Field & Uniform Electric Fields- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
Electric Potential in a Radial Field \( V = \dfrac{Q}{4\pi\varepsilon_0 r} \)
An isolated point charge produces a radial electric field. The electric potential at a distance from the charge depends on how far the point is from the charge.
Equation for Electric Potential in a Radial Field
The electric potential at a distance \( r \) from a point charge \( Q \) in free space is given by:
\( V = \dfrac{Q}{4\pi\varepsilon_0 r} \)
- \( V \) = electric potential (V)
- \( Q \) = charge producing the field (C)
- \( r \) = distance from the charge (m)
- \( \varepsilon_0 \) = permittivity of free space \( = 8.85\times10^{-12}\ \mathrm{F\,m^{-1}} \)
Meaning of the Equation
- Electric potential decreases with increasing distance from the charge.
- The potential is proportional to the magnitude of the charge.
- The potential is defined relative to zero at infinity.
Sign of the potential:
- If \( Q \) is positive, \( V \) is positive.
- If \( Q \) is negative, \( V \) is negative.
Radial Nature of the Field
- Equipotential surfaces are concentric spheres centred on the charge.
- Electric field lines are radial and perpendicular to equipotential surfaces.
- The electric field points from high potential to low potential.
Link Between Electric Potential and Electric Field
The electric field is related to the gradient of the potential:
\( E = -\dfrac{dV}{dr} \)
Differentiating the potential equation gives:
\( E = \dfrac{Q}{4\pi\varepsilon_0 r^2} \)
This matches the expression for electric field due to a point charge.
When This Equation Applies
- The charge is stationary.
- The charge can be treated as a point charge.
- The medium is free space or air.
- Distances are measured from the centre of the charge.
Example (Easy)
Calculate the electric potential at a point \( 0.50\ \mathrm{m} \) from a charge of \( 2.0\times10^{-6}\ \mathrm{C} \).
▶️ Answer / Explanation
\( V = \dfrac{2.0\times10^{-6}}{4\pi(8.85\times10^{-12})(0.50)} \)
\( V \approx 3.6\times10^{4}\ \mathrm{V} \)
Example (Medium)
The electric potential at a point is \( 1.8\times10^{4}\ \mathrm{V} \), located \( 0.40\ \mathrm{m} \) from a point charge. Find the magnitude of the charge.
▶️ Answer / Explanation
Rearrange the equation:
\( Q = 4\pi\varepsilon_0 rV \)
\( Q = 4\pi(8.85\times10^{-12})(0.40)(1.8\times10^{4}) \)
\( Q \approx 8.0\times10^{-7}\ \mathrm{C} \)
Example (Hard)
Explain what happens to the electric potential if the distance from a point charge is doubled.
▶️ Answer / Explanation
- Electric potential is inversely proportional to \( r \).
- Doubling \( r \) halves the potential.
- The sign of the potential remains the same.
Electric Field Lines and Equipotentials: Radial and Uniform Fields
Electric fields can be represented visually using field lines and equipotential lines (or surfaces). These diagrams help us understand the direction and strength of electric fields.
Electric Field Lines
- Show the direction of the electric field.
- Direction is the direction of force on a positive test charge.
- Field lines never cross.
- Closer field lines indicate a stronger electric field.
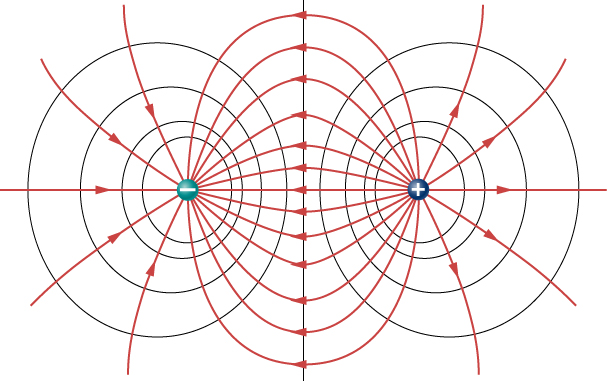
Equipotential Lines (or Surfaces)
- Join points of equal electric potential.
- No work is done moving a charge along an equipotential.
- Equipotentials are always perpendicular to electric field lines.
- Closer equipotentials indicate a stronger electric field.
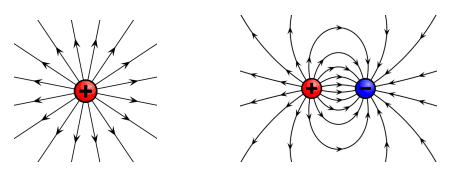
Radial Electric Field (Point Charge)
A radial electric field is produced by a point charge.
Field lines:
- Radiate symmetrically from the charge.
- Point away from a positive charge.
- Point towards a negative charge.
- Become less dense as distance increases → field strength decreases.
Equipotentials:
- Concentric circles (or spheres in 3D).
- Spacing increases with distance.
- Always perpendicular to field lines.
Interpretation:
- Field strength decreases with distance.
- Potential decreases with distance from a positive charge.
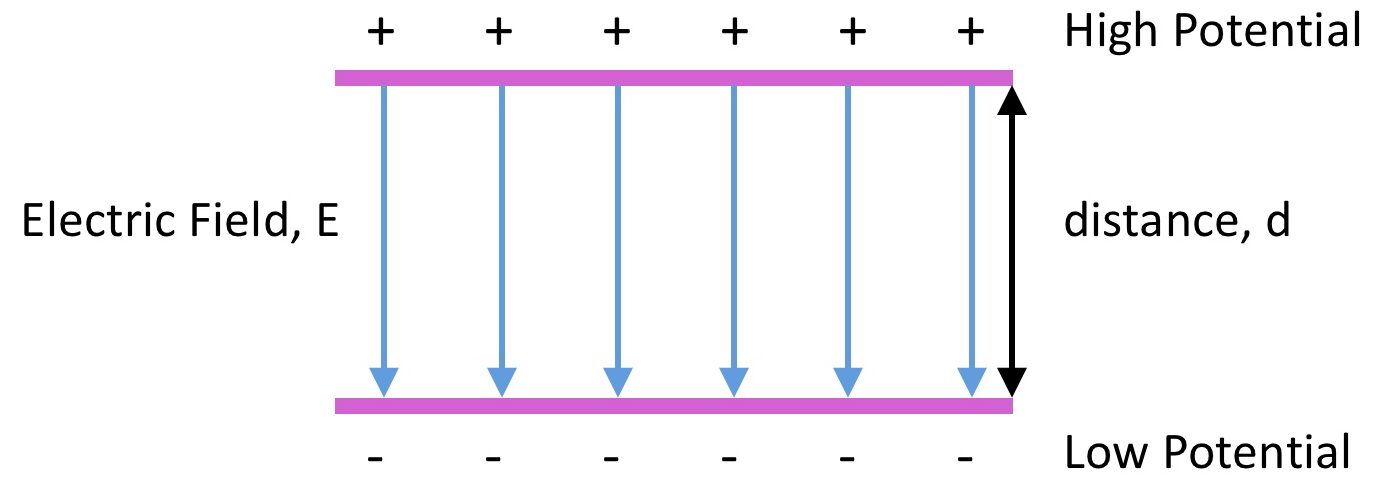
Uniform Electric Field (Parallel Plates)
A uniform electric field is produced between parallel charged plates.
Field lines:
- Straight, parallel, and equally spaced.
- Point from the positive plate to the negative plate.
- Equal spacing indicates constant field strength.
Equipotentials:
- Parallel to the plates.
- Equally spaced.
- Perpendicular to the field lines.
Interpretation:
- Electric field strength is constant.
- Potential changes linearly with distance.
Key Comparisons
| Feature | Radial Field | Uniform Field |
|---|---|---|
| Field line shape | Radial | Parallel straight lines |
| Field strength | Decreases with distance | Constant |
| Equipotentials | Concentric circles | Parallel lines |
| Spacing meaning | Closer → stronger field | Equal spacing → uniform field |
Exam Interpretation Tips
- Always state direction of field using arrows.
- Never allow field lines to cross.
- Ensure equipotentials meet field lines at right angles.
- Use spacing to indicate relative field strength.
Example (Easy)
Why are equipotential lines perpendicular to electric field lines?
▶️ Answer / Explanation
- Electric field points in direction of maximum potential decrease.
- Along an equipotential, potential is constant.
- Therefore, the field must be perpendicular.
Example (Medium)
A diagram shows radial field lines becoming closer near a charge. What does this indicate?
▶️ Answer / Explanation
- Field strength increases closer to the charge.
- Electric force on a charge would be larger.
Example (Hard)
Explain how you could identify a uniform electric field from a diagram.
▶️ Answer / Explanation
- Field lines are straight and parallel.
- Field lines are equally spaced.
- Equipotentials are parallel and equally spaced.