Edexcel A Level (IAL) Physics-4.24 Exponential Discharge in a Capacitor- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -4.24 Exponential Discharge in a Capacitor- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -4.24 Exponential Discharge in a Capacitor- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
- be able to use the equation \(Q=Q_0 e^{-t/RC}\) and derive and use related equations for exponential discharge in a resistor-capacitor circuit,
\(I=I_0 e^{-t/RC}\) and \(V=V_0 e^{-t/RC}\)
and the corresponding log equations
\(\ln Q=\ln Q_0-\dfrac{t}{RC}\),
\(\ln I=\ln I_0-\dfrac{t}{RC}\) and
\(\ln V=\ln V_0-\dfrac{t}{RC}\)
Exponential Discharge in an RC Circuit
When a charged capacitor discharges through a resistor, the charge, current, and potential difference all decrease exponentially with time. This behaviour is characterised by the time constant \( RC \).
Exponential Discharge of Charge
The charge on a discharging capacitor is given by:![]()
\( Q = Q_0 e^{-t/RC} \)
- \( Q \) = charge at time \( t \)
- \( Q_0 \) = initial charge
- \( R \) = resistance
- \( C \) = capacitance
- \( t \) = time
Interpretation:
- Charge decreases rapidly at first, then more slowly.
- After one time constant \( RC \), charge falls to about 37% of \( Q_0 \).
Exponential Discharge of Current
Current is proportional to the rate of flow of charge:
\( I = \dfrac{\mathrm{d}Q}{\mathrm{d}t} \)
For a discharging capacitor, current also decreases exponentially:
\( I = I_0 e^{-t/RC} \)
- \( I_0 \) = initial current
Key point: Current is maximum at the start of discharge and approaches zero as time increases.
Exponential Discharge of Potential Difference
Using the capacitance equation \( Q = CV \):
\( V = \dfrac{Q}{C} \)
Substitute \( Q = Q_0 e^{-t/RC} \):
\( V = V_0 e^{-t/RC} \)
- \( V_0 \) = initial voltage across the capacitor
After one time constant:
- \( V = 0.37V_0 \)
Logarithmic Forms of the Discharge Equations
Taking the natural logarithm of the exponential equations allows straight-line graph analysis.
Charge:
\( \ln Q = \ln Q_0 – \dfrac{t}{RC} \)
Current:
\( \ln I = \ln I_0 – \dfrac{t}{RC} \)
Voltage:
\( \ln V = \ln V_0 – \dfrac{t}{RC} \)
Graphical Interpretation
If \( \ln Q \), \( \ln I \), or \( \ln V \) is plotted against time \( t \):
- The graph is a straight line.
- The gradient is \( -\dfrac{1}{RC} \).
- The y-intercept gives \( \ln Q_0 \), \( \ln I_0 \), or \( \ln V_0 \).
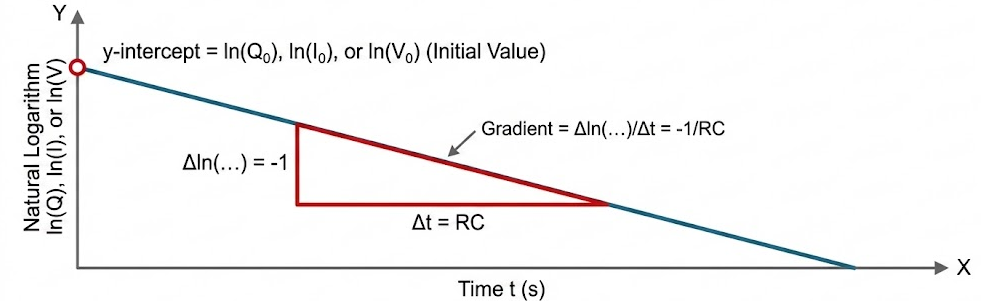
This method allows the time constant to be determined experimentally.
Determining the Time Constant from a Graph
From the gradient:
\( \text{gradient} = -\dfrac{1}{RC} \)
Therefore:
\( RC = -\dfrac{1}{\text{gradient}} \)
Example (Easy)
A capacitor has time constant \( 5.0\ \mathrm{s} \). Find the fraction of charge remaining after \( 5.0\ \mathrm{s} \).
▶️ Answer / Explanation
\( \dfrac{Q}{Q_0} = e^{-t/RC} = e^{-1} \approx 0.37 \)
37% of the initial charge remains.
Example (Medium)
A capacitor initially at \( 10\ \mathrm{V} \) discharges with time constant \( 2.0\ \mathrm{s} \). Find the voltage after \( 4.0\ \mathrm{s} \).
▶️ Answer / Explanation
\( V = V_0 e^{-t/RC} = 10 e^{-4/2} = 10e^{-2} \approx 1.35\ \mathrm{V} \)
Example (Hard)
A graph of \( \ln V \) against time has a gradient of \( -0.25\ \mathrm{s^{-1}} \). Determine the time constant of the circuit.
▶️ Answer / Explanation
\( RC = -\dfrac{1}{\text{gradient}} = \dfrac{1}{0.25} = 4.0\ \mathrm{s} \)
