Edexcel A Level (IAL) Physics-4.35 Radius of a Charged Particle in a Magnetic Field- Study Notes- New Syllabus

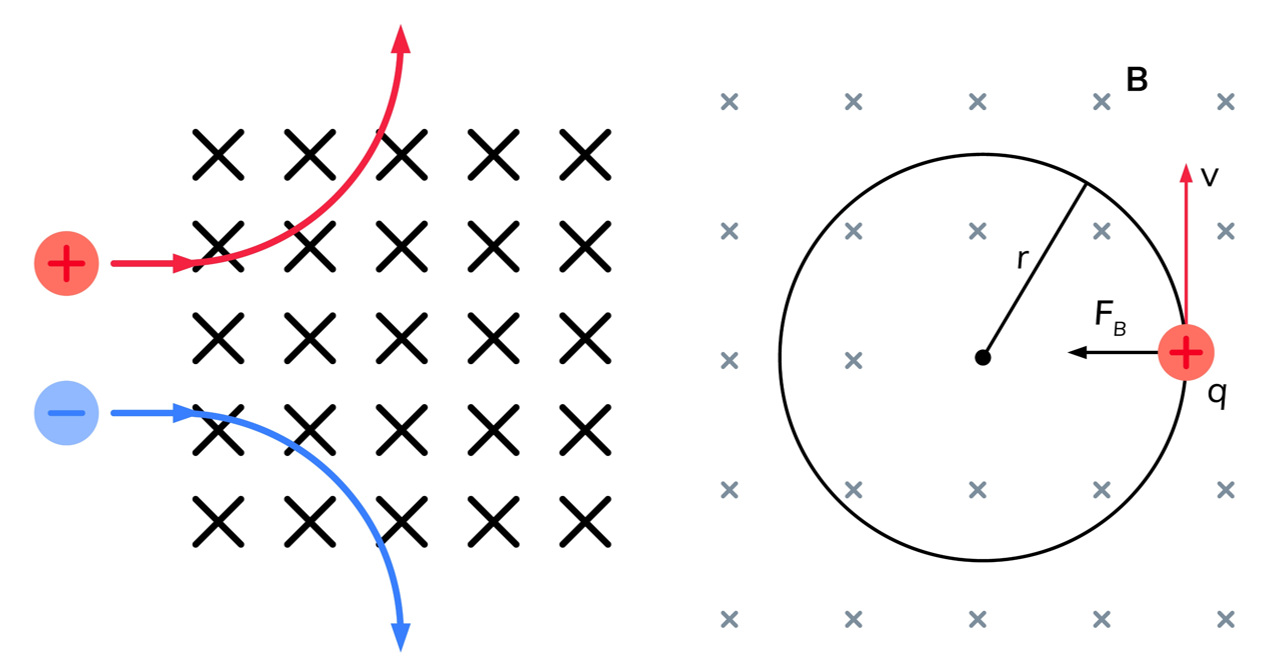
Radius of Circular Motion of a Charged Particle in a Magnetic Field

When a charged particle moves through a uniform magnetic field with its velocity perpendicular to the field, it follows a circular path. The radius of this path depends on the particle’s momentum, the magnetic flux density, and the charge.

 Magnetic Force on a Moving Charged Particle

The magnetic force acting on a charged particle moving perpendicular to a magnetic field is:

\( F = BQv \)

• \( B \) = magnetic flux density (T)
• \( Q \) = charge of the particle (C)
• \( v \) = speed of the particle (m s⁻¹)

Centripetal Force for Circular Motion

For circular motion of radius \( r \), the required centripetal force is:

\( F = \dfrac{mv^2}{r} \)

• \( m \) = mass of the particle (kg)
• \( r \) = radius of the circular path (m)

Derivation of \( r = \dfrac{p}{BQ} \)

In a magnetic field, the magnetic force provides the centripetal force:

\( BQv = \dfrac{mv^2}{r} \)

Rearranging:

\( r = \dfrac{mv}{BQ} \)

Since momentum \( p \) is defined as:

\( p = mv \)

Substitute \( p \) into the equation:

\( r = \dfrac{p}{BQ} \)

Meaning of the Equation

• Larger momentum → larger radius.
• Stronger magnetic field → smaller radius.
• Greater charge → smaller radius.
• Magnetic field changes direction of motion, not speed.

Conditions for the Equation

• Magnetic field is uniform.
• Particle velocity is perpendicular to the magnetic field.
• Speed remains constant.

 Applications

• Mass spectrometers
• Cyclotrons
• Particle detectors
• Determining momentum of charged particles