Edexcel A Level (IAL) Physics-4.38 Annihilation of Matter & Antimatter- Study Notes- New Syllabus

Mass–Energy Equivalence in Particle Creation and Annihilation

Einstein’s mass–energy equivalence shows that mass and energy are interchangeable. In particle physics, this principle explains the creation and annihilation of matter–antimatter pairs.

 Mass–Energy Equivalence

The change in energy associated with a change in mass is given by:

\( \Delta E = c^2 \Delta m \)

• \( \Delta E \) = change in energy (J)
• \( \Delta m \) = change in mass (kg)
• \( c \) = speed of light in vacuum

This equation applies whenever mass is created from energy or converted into energy.

Annihilation of Matter and Antimatter 

Annihilation occurs when a particle meets its antiparticle.

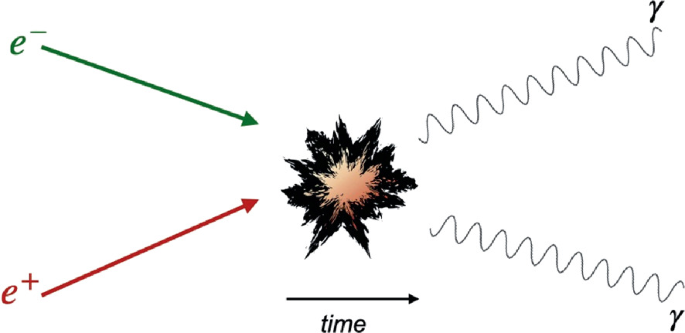
• The particle and antiparticle destroy each other.
• Their rest mass is converted into energy.
• Energy is usually released as gamma-ray photons.

Example:

Electron + Positron → gamma radiation

The total energy released is:

\( \Delta E = c^2 (m_{\text{electron}} + m_{\text{positron}}) \)

Creation of Matter–Antimatter Pairs (Pair Production)

Pair production is the reverse process of annihilation.

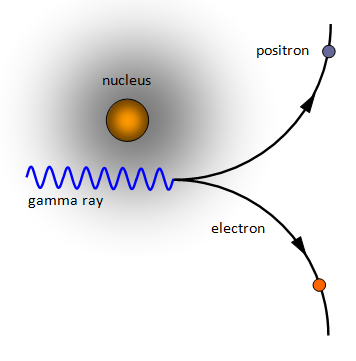
• A high-energy photon can create a particle–antiparticle pair.
• The photon must have at least the energy equivalent to the rest mass of the pair.
• Occurs near a nucleus to conserve momentum.

Minimum energy condition:

\( E_{\text{photon}} \ge c^2 (m_{\text{particle}} + m_{\text{antiparticle}}) \)

Using \( \Delta E = c^2 \Delta m \) in Calculations

To apply the equation:

1. Identify the change in mass \( \Delta m \).
2. Substitute into \( \Delta E = c^2 \Delta m \).
3. Calculate the energy released or required.

Important Points

• Mass is not conserved separately — mass–energy is conserved.
• Even a small mass change corresponds to a very large energy change.
• This explains the large energies involved in nuclear and particle processes.