Edexcel A Level (IAL) Physics-4.4 Core Practical 10: Investigating Collisions using ICT- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -4.4 Core Practical 10: Investigating Collisions using ICT- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -4.4 Core Practical 10: Investigating Collisions using ICT- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
- CORE PRACTICAL 10: Use ICT to analyse collisions between small spheres, e.g. ball bearings on a table top
CORE PRACTICAL 10: Use ICT to Analyse Collisions Between Small Spheres
Aim
To analyse collisions between small spheres using ICT and verify conservation of linear momentum in two dimensions.
Theory
Momentum is defined as:
\( p = mv \)
For an isolated system:
Total momentum before collision = total momentum after collision
In two dimensions, momentum is conserved independently in perpendicular directions:
\( \sum p_x = \text{constant} \)
\( \sum p_y = \text{constant} \)
Apparatus
- Small spheres (ball bearings)
- Smooth horizontal surface (air table or low-friction tabletop)
- Video camera or smartphone
- Motion analysis software (e.g. Tracker)
- Ruler or scale for calibration
- White background and good lighting
Method
- Set up the table with a scale visible for distance calibration.
- Position the camera directly above the table to minimise parallax error.
- Record a video of one sphere colliding with another (initially at rest or moving).
- Import the video into motion analysis software.
- Calibrate the scale using the known length in the video.
- Track the positions of each sphere frame by frame before and after the collision.
- Use the software to calculate velocities in the x and y directions.
Data Processing
Calculate momentum components:
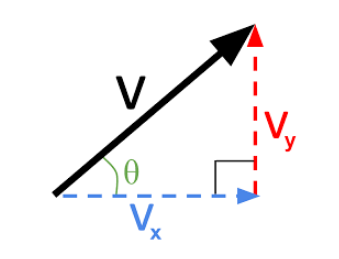
\( p_x = mv_x \)
\( p_y = mv_y \)
Calculate total momentum before and after the collision for each direction.
Expected Results
- Total momentum in the x-direction is conserved.
- Total momentum in the y-direction is conserved.
- Small differences may occur due to friction and measurement uncertainty.
Example Results Table
| Sphere | \( v_x \) (m s⁻¹) | \( v_y \) (m s⁻¹) | \( p_x \) (kg m s⁻¹) | \( p_y \) (kg m s⁻¹) |
|---|---|---|---|---|
| Before (1) | 0.40 | 0 | 0.008 | 0 |
| After (1) | 0.20 | 0.15 | 0.004 | 0.003 |
| After (2) | 0.20 | -0.15 | 0.004 | -0.003 |
Result: Total momentum before ≈ total momentum after (within uncertainty).
Safety Considerations
- Ensure spheres cannot roll off the table.
- Keep the working area clear.
- Avoid eye-level collisions with moving objects.
Sources of Error and Improvements
- Parallax error: camera not directly above → place camera vertically.
- Friction: use smooth or air table to reduce losses.
- Frame rate limits: use high-frame-rate video for accuracy.
- Tracking error: ensure good contrast and lighting.
Conclusion
- ICT allows accurate measurement of velocity in two dimensions.
- Momentum conservation is verified experimentally.
- The experiment supports Newton’s laws of motion.
