Edexcel A Level (IAL) Physics-4.6 Energy–Momentum Relation- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -4.6 Energy–Momentum Relation- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -4.6 Energy–Momentum Relation- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
- be able to derive and use the equation \( E_k = \dfrac{p^2}{2m} \) for the kinetic energy of a non- relativistic particle
Kinetic Energy of a Non-Relativistic Particle: \( E_k = \dfrac{p^2}{2m} \)
This section shows how to derive and use the kinetic energy–momentum relation for a non-relativistic particle (i.e. when the speed is much less than the speed of light).
Definitions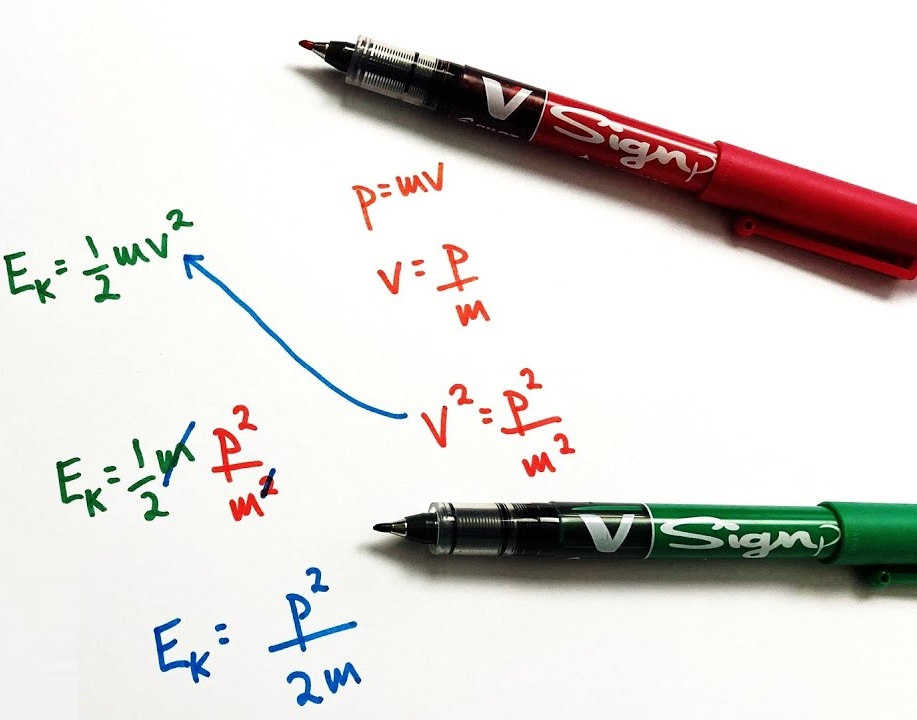
Momentum is defined as:
\( p = mv \)
Kinetic energy is defined as:
\( E_k = \dfrac{1}{2}mv^2 \)
Derivation of \( E_k = \dfrac{p^2}{2m} \)
From the momentum definition:
\( v = \dfrac{p}{m} \)
Substitute this into the kinetic energy equation:
\( E_k = \dfrac{1}{2}m\left(\dfrac{p}{m}\right)^2 \)
Simplify:
\( E_k = \dfrac{1}{2}m \cdot \dfrac{p^2}{m^2} = \dfrac{p^2}{2m} \)
Result:
\( E_k = \dfrac{p^2}{2m} \)
Conditions of Validity
- Particle speed \( v \ll c \) (speed of light).
- Relativistic effects are negligible.
- Applies to everyday objects, electrons at low speeds, and most mechanics problems.
Note: At very high speeds, relativistic expressions must be used instead.
Why This Form Is Useful
- Allows kinetic energy to be calculated directly from momentum.
- Useful when momentum is known but velocity is not.
- Important in particle physics, electron diffraction, and quantum contexts.
Units Check
Momentum has units \( \mathrm{kg\,m\,s^{-1}} \).
\( \dfrac{p^2}{2m} \rightarrow \dfrac{(\mathrm{kg^2\,m^2\,s^{-2}})}{\mathrm{kg}} = \mathrm{kg\,m^2\,s^{-2}} = \mathrm{J} \)
This confirms the expression gives energy in joules.
Example (Easy)
A particle has momentum \( 4.0\ \mathrm{kg\,m\,s^{-1}} \) and mass \( 2.0\ \mathrm{kg} \). Find its kinetic energy.
▶️ Answer / Explanation
\( E_k = \dfrac{p^2}{2m} = \dfrac{4.0^2}{2 \times 2.0} = \dfrac{16}{4} = 4.0\ \mathrm{J} \)
Example (Medium)
An electron of mass \( 9.11\times10^{-31}\ \mathrm{kg} \) has momentum \( 3.0\times10^{-24}\ \mathrm{kg\,m\,s^{-1}} \). Calculate its kinetic energy.
▶️ Answer / Explanation
\( E_k = \dfrac{(3.0\times10^{-24})^2}{2 \times 9.11\times10^{-31}} \)
\( E_k = \dfrac{9.0\times10^{-48}}{1.82\times10^{-30}} \approx 4.95\times10^{-18}\ \mathrm{J} \)
Example (Hard)
A particle has kinetic energy \( 20\ \mathrm{J} \) and mass \( 5.0\ \mathrm{kg} \). Find its momentum.
▶️ Answer / Explanation
Rearrange:
\( p = \sqrt{2mE_k} \)
\( p = \sqrt{2 \times 5.0 \times 20} = \sqrt{200} \approx 14.1\ \mathrm{kg\,m\,s^{-1}} \)
