Edexcel A Level (IAL) Physics-4.8 Angular Velocity- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -4.8 Angular Velocity- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -4.8 Angular Velocity- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
- understand what is meant by angular velocity and be able to use the equations \( v = \omega r \) and \( T = \dfrac{2\pi}{\omega} \)
Angular Velocity and Circular Motion
Angular velocity describes how quickly an object rotates about a fixed axis. It is a key quantity in circular motion and links rotational motion to linear motion.
Definition of Angular Velocity
Angular velocity \( \omega \) is defined as the rate of change of angular displacement.
![]()
\( \omega = \dfrac{\Delta \theta}{\Delta t} \)
- \( \omega \) = angular velocity (rad s⁻¹)
- \( \Delta \theta \) = angular displacement (radians)
- \( \Delta t \) = time taken (s)
Key point: Angular velocity is measured in radians per second.
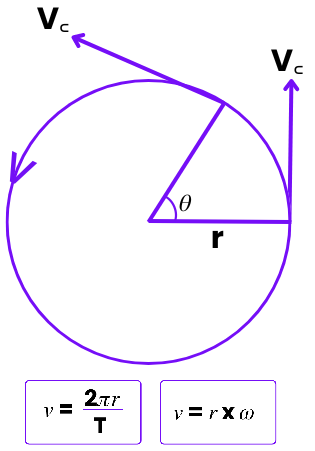
Relationship Between Linear Speed and Angular Velocity
![]()
For an object moving in a circle of radius \( r \):
\( v = \omega r \)
- \( v \) = linear (tangential) speed (m s⁻¹)
- \( \omega \) = angular velocity (rad s⁻¹)
- \( r \) = radius of circular path (m)
Important consequences:
- All points on a rotating object have the same angular velocity.
- Points further from the centre move faster linearly.
- Doubling the radius doubles the linear speed for the same \( \omega \).
Period of Circular Motion
The period \( T \) is the time taken for one complete revolution.
One full revolution corresponds to an angular displacement of \( 2\pi \) radians.
\( \omega = \dfrac{2\pi}{T} \)
Rearranging:
\( T = \dfrac{2\pi}{\omega} \)
- \( T \) = period (s)
- \( \omega \) = angular velocity (rad s⁻¹)
Connection with Frequency
Frequency \( f \) is the number of revolutions per second.
\( f = \dfrac{1}{T} \)
Combining with angular velocity:
\( \omega = 2\pi f \)
Example (Easy)
A wheel rotates at an angular velocity of \( 4.0\ \mathrm{rad\,s^{-1}} \). Find its period.
▶️ Answer / Explanation
\( T = \dfrac{2\pi}{\omega} = \dfrac{2\pi}{4.0} = 1.57\ \mathrm{s} \)
Example (Medium)
A particle moves in a circle of radius \( 0.50\ \mathrm{m} \) with angular velocity \( 6.0\ \mathrm{rad\,s^{-1}} \). Calculate its linear speed.
▶️ Answer / Explanation
\( v = \omega r = 6.0 \times 0.50 = 3.0\ \mathrm{m\,s^{-1}} \)
Example (Hard)
A point on the rim of a rotating disc moves at \( 10\ \mathrm{m\,s^{-1}} \). If the disc radius is \( 0.40\ \mathrm{m} \), find:
- (a) the angular velocity
- (b) the period of rotation
▶️ Answer / Explanation
(a) Angular velocity:
\( \omega = \dfrac{v}{r} = \dfrac{10}{0.40} = 25\ \mathrm{rad\,s^{-1}} \)
(b) Period:
\( T = \dfrac{2\pi}{\omega} = \dfrac{2\pi}{25} \approx 0.25\ \mathrm{s} \)
