Edexcel A Level (IAL) Physics-5.13 Background Radiation- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -5.13 Background Radiation- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -5.13 Background Radiation- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
Background Radiation and How to Take It into Account
Background radiation is the low-level ionising radiation that is always present in the environment, even when no radioactive source is nearby.
Sources of Background Radiation
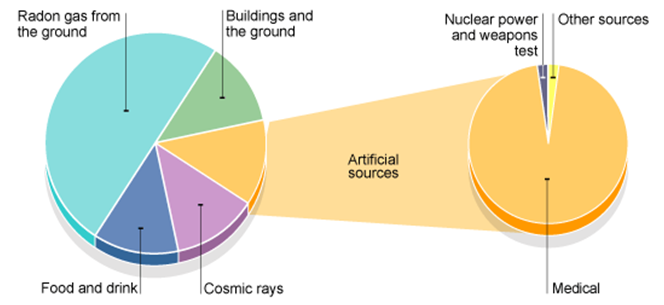
- Cosmic radiation from space
- Natural radioactivity from rocks, soil, and buildings
- Radon gas in the air
- Food and the human body (e.g. potassium-40)
Key point: Background radiation is always present and cannot be completely eliminated.
Why Background Radiation Must Be Accounted For
- Radiation detectors (e.g. Geiger–Müller tubes) detect all radiation.
- This includes radiation from both the source and the environment.
- Failing to correct for background radiation gives inaccurate results.
Therefore: Measured count rate = source radiation + background radiation.
Measuring Background Radiation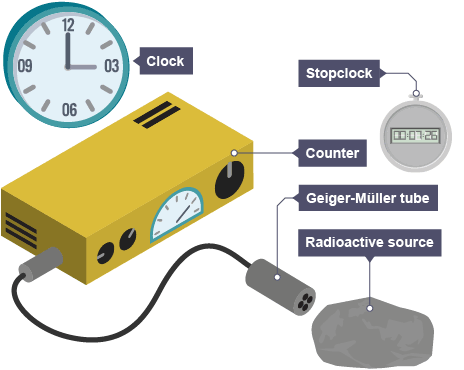
To measure background radiation:
- Remove all radioactive sources from the detector.
- Record counts over a fixed time interval.
- Repeat measurements and find an average.
This gives the background count rate.
Correcting for Background Radiation
The true count rate from the source is found by subtracting the background count rate:
\( \text{corrected count rate} = \text{measured count rate} – \text{background count rate} \)
Important: Both counts must be measured over the same time interval.
Example of Background Correction
- Measured count = 240 counts in 60 s
- Background count = 60 counts in 60 s
Corrected count:
\( \text{corrected count} = 240 – 60 = 180 \)
Corrected count rate:
\( \text{corrected count rate} = \dfrac{180}{60} = 3.0\ \mathrm{counts\,s^{-1}} \)
Importance in Half-Life Experiments
- As a radioactive source decays, its count rate decreases.
- Eventually, measured count rate approaches background level.
- Background must be subtracted at every stage.
- Failure to do so causes errors in half-life calculations.
Key warning: When corrected count rate approaches zero, results become unreliable.
Safety and Good Practice
- Always measure background radiation first.
- Use long counting times to reduce random uncertainty.
- Repeat measurements and average results.
- Keep radioactive sources shielded when not in use.
Example (Easy)
A detector records 150 counts in 50 s. Background radiation gives 30 counts in 50 s. Find the corrected count rate.
▶️ Answer / Explanation
Corrected counts:
\( 150 – 30 = 120 \)
Corrected count rate:
\( \dfrac{120}{50} = 2.4\ \mathrm{counts\,s^{-1}} \)
Example (Medium)
Explain why background radiation becomes more significant when measuring weak radioactive sources.
▶️ Answer / Explanation
- The source count rate is small.
- Background radiation becomes a larger fraction of total counts.
- Small errors in background subtraction cause large percentage errors.
Example (Hard)
A radioactive source gives a measured count rate of \( 1.2\ \mathrm{counts\,s^{-1}} \). Background radiation is \( 0.9\ \mathrm{counts\,s^{-1}} \). Explain why this result is unreliable.
▶️ Answer / Explanation
- Corrected count rate is very small.
- Random fluctuations in background dominate the measurement.
- Percentage uncertainty is very high.
- Results near background level are unreliable.