Edexcel A Level (IAL) Physics-5.18 Equations for Nuclear Physics- Study Notes- New Syllabus

Half-Life, Radioactive Decay Equations and Logarithmic Forms

Radioactive decay describes how the number of unstable nuclei and the activity of a radioactive source decrease with time. This behaviour can be analysed graphically and using exponential and logarithmic equations.

Activity and Number of Nuclei

Activity is the rate at which nuclei decay.

\( A = \lambda N \)

• \( A \) = activity (Bq)
• \( N \) = number of undecayed nuclei
• \( \lambda \) = decay constant (s⁻¹)

Meaning: Higher number of nuclei → higher activity.

Radioactive Decay Law

The rate of decay of nuclei is proportional to the number remaining:

\( \dfrac{dN}{dt} = -\lambda N \)

• Negative sign indicates that \( N \) decreases with time.
• The decay constant \( \lambda \) is a property of the isotope.

 Exponential Decay Equation

Solving the decay equation gives:

\( N = N_0 e^{-\lambda t} \)

• \( N_0 \) = initial number of nuclei
• \( t \) = time

Since activity is proportional to \( N \):

\( A = A_0 e^{-\lambda t} \)

 Half-Life and Decay Constant

Half-life \( t_{1/2} \) is the time taken for half the nuclei to decay.

The relationship between half-life and decay constant is:

\( \lambda = \dfrac{\ln 2}{t_{1/2}} \)

Important: Half-life is constant for a given isotope.

Determining Half-Life Graphically

Method:

• Plot activity (or count rate) against time.
• Subtract background radiation first.
• Choose any value of activity.
• Find the time taken for activity to fall to half that value.
• This time interval is the half-life.

Note: The half-life is the same anywhere on the decay curve.

Logarithmic Form of the Decay Equation

Starting from:

\( N = N_0 e^{-\lambda t} \)

Take natural logarithms:

\( \ln N = \ln N_0 – \lambda t \)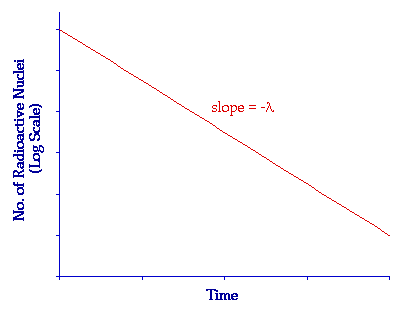

Similarly for activity:

\( \ln A = \ln A_0 – \lambda t \)

Using Log Graphs

• Plot \( \ln A \) against \( t \).
• The graph is a straight line.
• Gradient = \( -\lambda \).
• Intercept = \( \ln A_0 \).

Half-life can then be found using:

\( t_{1/2} = \dfrac{\ln 2}{\lambda} \)