Edexcel A Level (IAL) Physics-5.21 Period of Simple Harmonic Oscillators- Study Notes- New Syllabus

Periods of a Simple Harmonic Oscillator and a Simple Pendulum

The time period of an object undergoing simple harmonic motion (SHM) depends on the physical properties of the system. Two important SHM systems are the mass–spring system and the simple pendulum.

 Simple Harmonic Oscillator (Mass–Spring System)

For a mass attached to a spring oscillating vertically or horizontally (within the elastic limit), the period is:

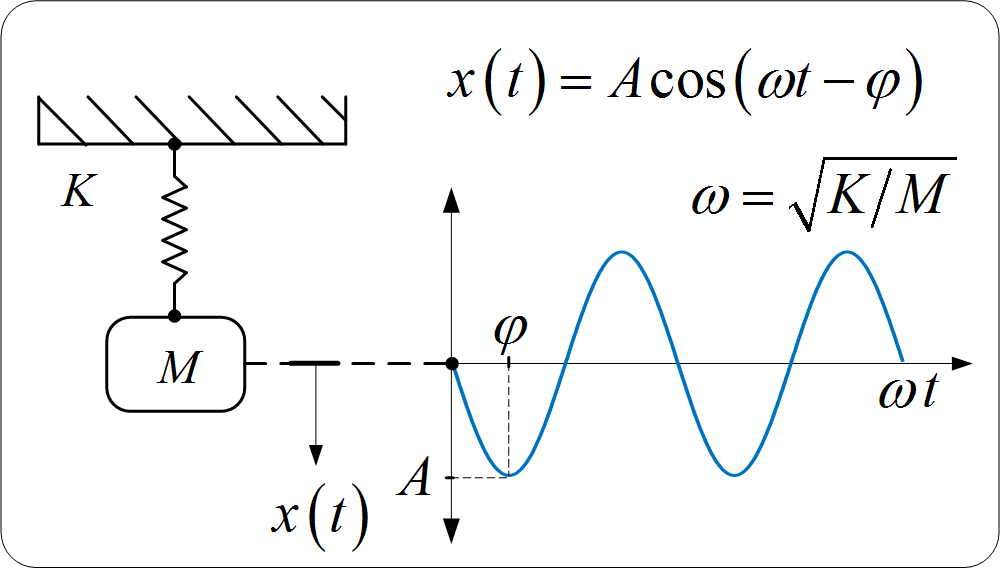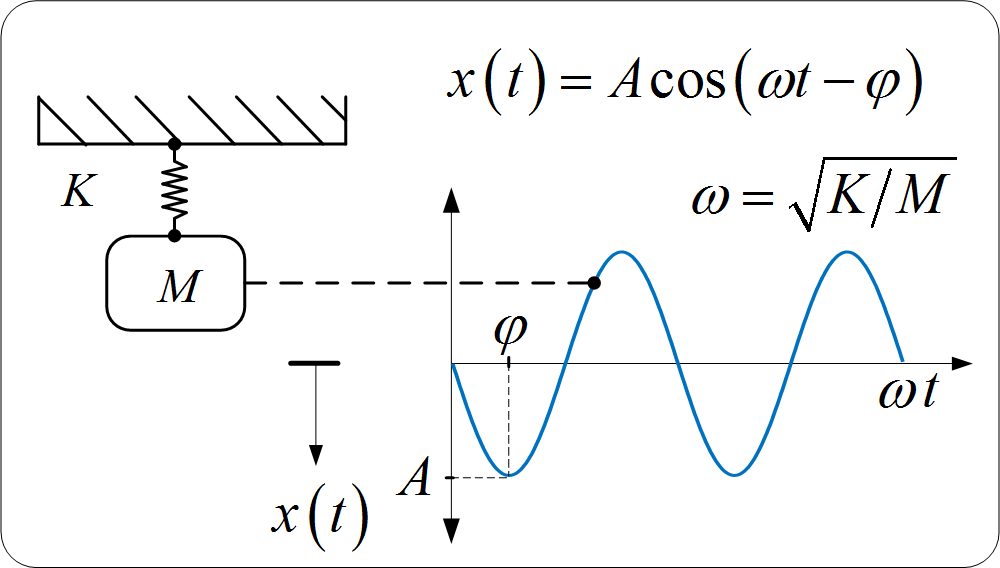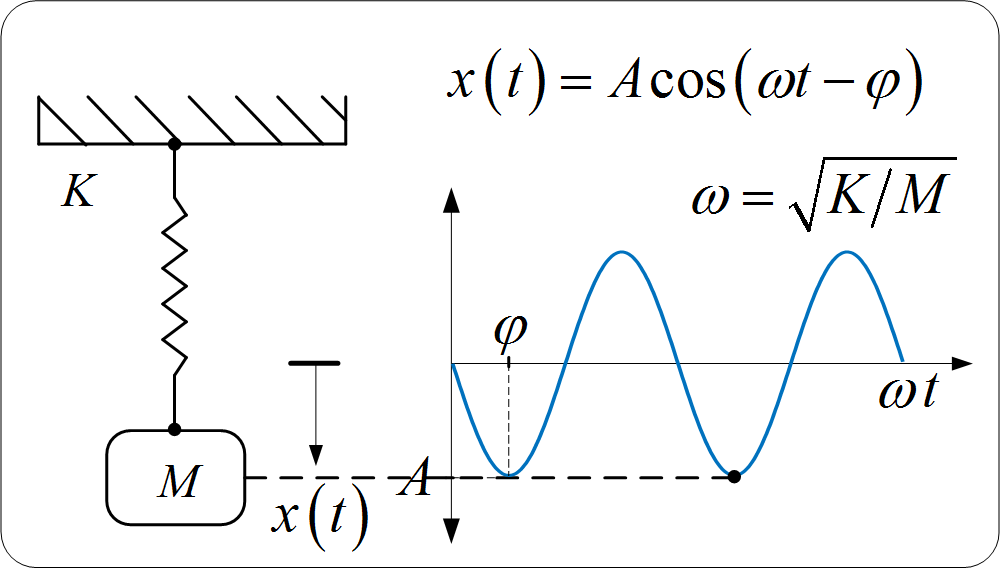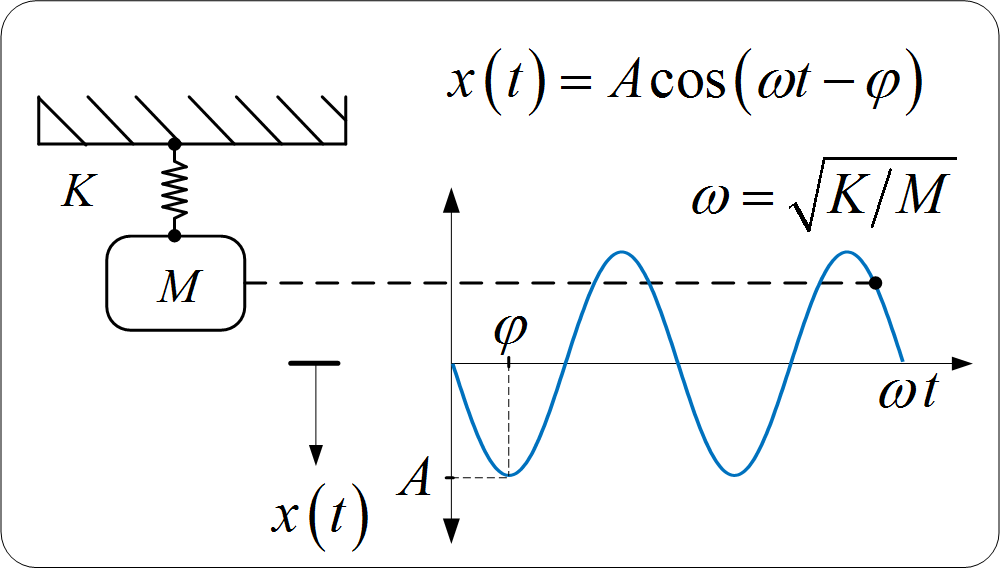
\( T = 2\pi \sqrt{\dfrac{m}{k}} \)

• \( T \) = period of oscillation (s)
• \( m \) = mass attached to the spring (kg)
• \( k \) = spring constant (N m⁻¹)

Key points:

• The period increases with increasing mass.
• The period decreases with a stiffer spring (larger \( k \)).
• The period is independent of amplitude (for SHM).
• Gravity does not affect the period of a horizontal spring system.

 Simple Pendulum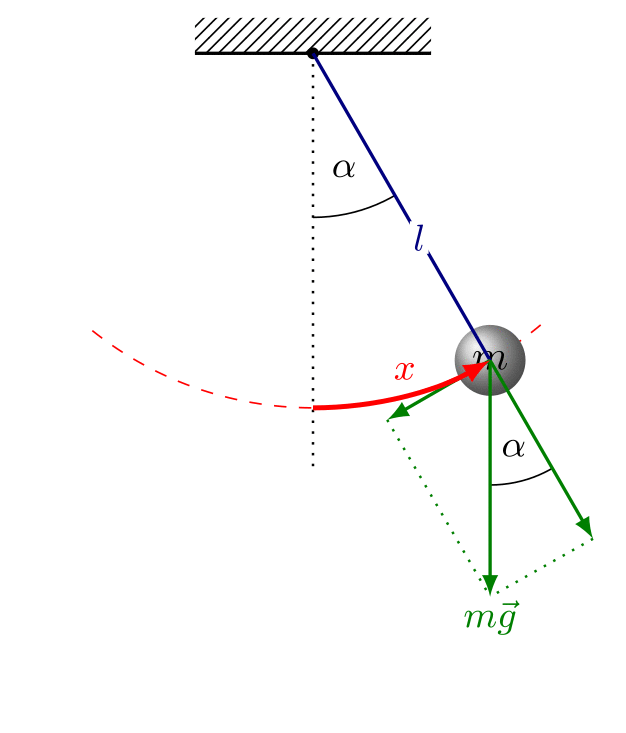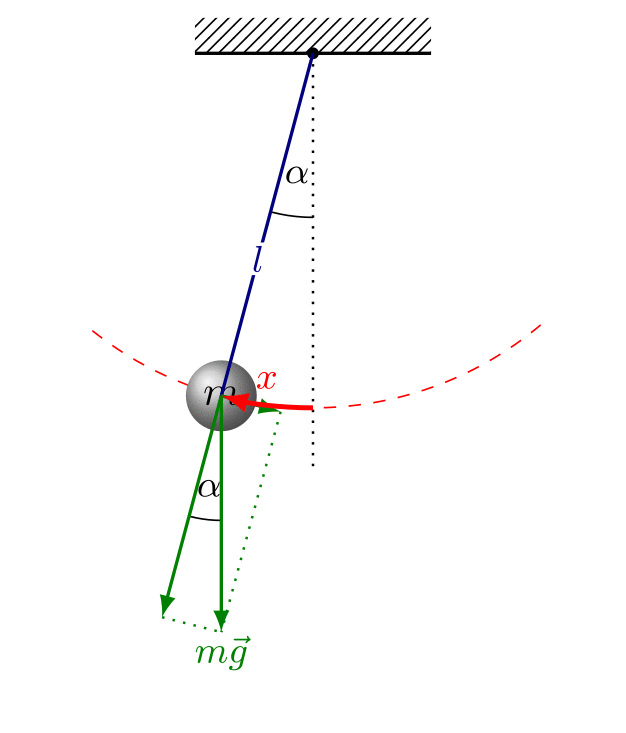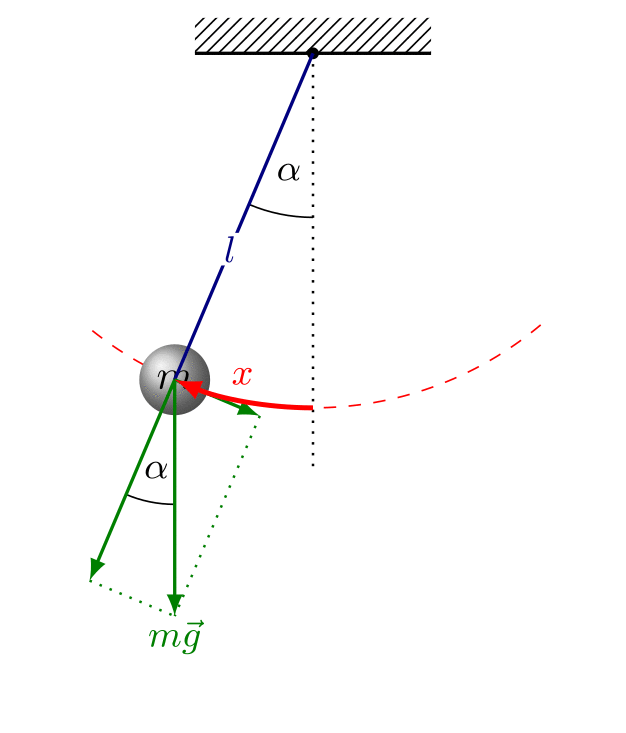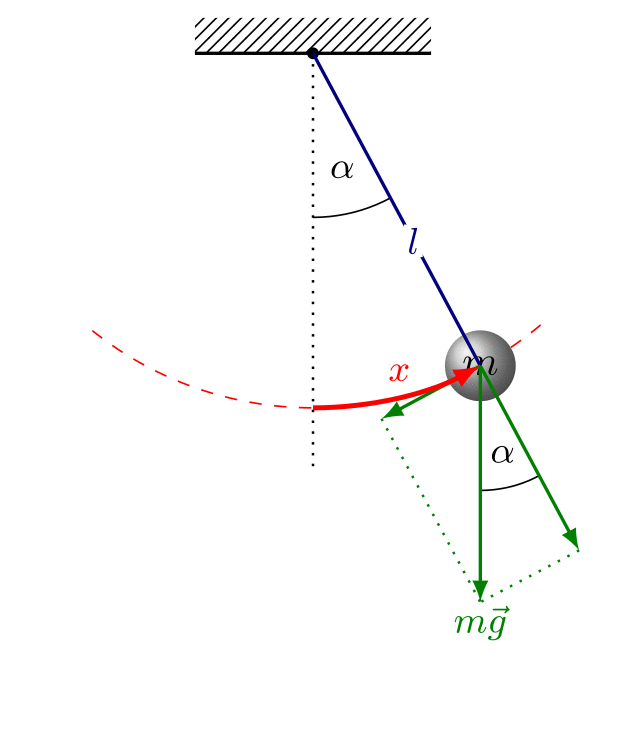

A simple pendulum consists of a small mass (bob) suspended by a light, inextensible string.

For small angular displacements, the period is:

\( T = 2\pi \sqrt{\dfrac{l}{g}} \)

• \( T \) = period of oscillation (s)
• \( l \) = length of the pendulum (m)
• \( g \) = gravitational field strength (m s⁻²)

Conditions:

• Angular displacement must be small (typically less than \( 10^\circ \)).
• The string must be light and inextensible.

Comparison of the Two Systems

• Mass–spring system depends on \( m \) and \( k \).
• Pendulum depends on \( l \) and \( g \).
• Neither system depends on amplitude for SHM.
• Pendulum period increases if gravity is weaker.

 Using the Equations

• Ensure SI units are used.
• Check that SHM conditions are satisfied.
• Rearrange equations carefully when solving for unknowns.