Edexcel A Level (IAL) Physics-5.25 Core Practical 16: Investigating Resonance- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -5.25 Core Practical 16: Investigating Resonance- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -5.25 Core Practical 16: Investigating Resonance- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
CORE PRACTICAL 16: Determine the value of an unknown mass using the resonant frequencies of the oscillation of known masses
CORE PRACTICAL 16: Determining an Unknown Mass Using Resonant Frequencies
This experiment uses resonance in a mass–spring system to determine the value of an unknown mass by comparing its resonant frequency with those of known masses.
Aim
To determine the value of an unknown mass by measuring resonant frequencies for different known masses and using the relationship between frequency and mass.
Theory
For a mass–spring system undergoing simple harmonic motion, the period is given by:
\( T = 2\pi \sqrt{\dfrac{m}{k}} \)
Since frequency \( f = \dfrac{1}{T} \):
\( f = \dfrac{1}{2\pi} \sqrt{\dfrac{k}{m}} \)
Rearranging gives:
\( f^2 \propto \dfrac{1}{m} \)
Key idea: Resonance occurs when the driving frequency equals the natural frequency of the mass–spring system, producing maximum amplitude.
Apparatus
- Spring
- Mass hanger and known slotted masses
- Unknown mass
- Signal generator
- Vibration driver
- Clamp stand
- Metre rule
Method
- Attach the spring to the vibration driver.
- Attach a known mass to the lower end of the spring.
- Increase the driving frequency gradually.
- Identify the resonant frequency where the amplitude is maximum.
- Record the resonant frequency for that mass.
- Repeat for several different known masses.
- Replace the known mass with the unknown mass.
- Find the resonant frequency of the unknown mass.
Analysis
- Calculate \( f^2 \) for each known mass.
- Plot a graph of \( f^2 \) against \( \dfrac{1}{m} \).
- The graph should be a straight line.
Using the graph:
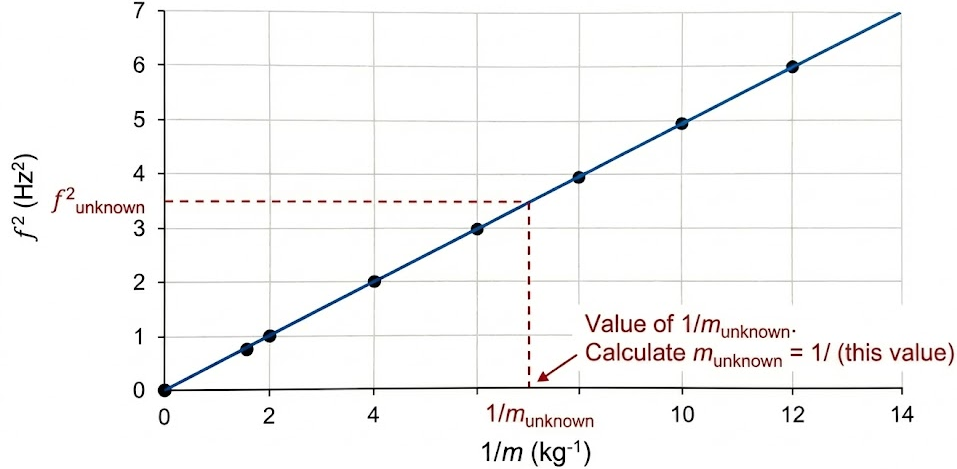
- Find \( \dfrac{1}{m} \) corresponding to the unknown mass frequency.
- Determine the unknown mass from the graph.
Safety Precautions
- Ensure masses are securely attached.
- Do not overstretch the spring.
- Switch off the signal generator when adjusting the setup.
Sources of Error
- Difficulty identifying exact resonance
- Damping due to air resistance
- Inaccurate mass values
- Non-vertical oscillations
Improvements
- Use a larger number of known masses.
- Repeat frequency measurements and average.
- Reduce damping using a heavier driver.
- Ensure oscillations remain vertical.
Example
A known mass of \( 0.50\,\mathrm{kg} \) resonates at \( 2.0\,\mathrm{Hz} \). An unknown mass resonates at \( 1.6\,\mathrm{Hz} \).
Find the unknown mass.
▶️ Answer / Explanation
Using \( f^2 \propto \dfrac{1}{m} \):
\( \dfrac{f_1^2}{f_2^2} = \dfrac{m_2}{m_1} \)
\( \dfrac{2.0^2}{1.6^2} = \dfrac{m}{0.50} \)
\( m = 0.78\,\mathrm{kg} \)
Conclusion
- Resonance occurs at the natural frequency of the system.
- Resonant frequency depends on mass.
- An unknown mass can be accurately determined using resonance.
