Edexcel A Level (IAL) Physics-5.39 Wien’s Law- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -5.39 Wien’s Law- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -5.39 Wien’s Law- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
Wien’s Displacement Law for Black Body Radiators
Wien’s displacement law describes how the wavelength at which a black body emits maximum radiation depends on its temperature.
Wien’s Displacement Law
The relationship between peak wavelength and absolute temperature is: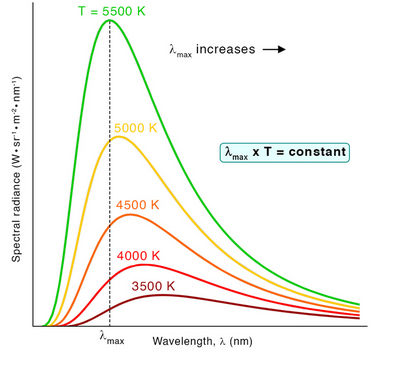
\( \lambda_{\text{max}} T = 2.898 \times 10^{-3}\,\mathrm{m\,K} \)
- \( \lambda_{\text{max}} \) = wavelength of maximum intensity (m)
- \( T \) = absolute temperature (K)
- \( 2.898 \times 10^{-3}\,\mathrm{m\,K} \) = Wien’s constant
Meaning of the Equation
- As temperature increases, peak wavelength decreases.
- Hotter objects emit radiation with shorter wavelengths.
- Cooler objects emit radiation with longer wavelengths.
Key idea:
- Peak wavelength is inversely proportional to temperature.
Physical Interpretation
- Low-temperature objects emit mainly infrared radiation.
- As temperature rises, emission moves through visible light.
- Very hot objects emit ultraviolet radiation.
This explains why:
- Warm objects are invisible to the eye.
- Red-hot objects glow red.
- Very hot stars appear blue.
Using Wien’s Law in Calculations
- Temperature must be in kelvin.
- Peak wavelength must be in metres.
- Rearrange the equation carefully.
Rearranged forms:
\( \lambda_{\text{max}} = \dfrac{2.898 \times 10^{-3}}{T} \)
\( T = \dfrac{2.898 \times 10^{-3}}{\lambda_{\text{max}}} \)
Link to Radiation Curves
- Each radiation curve has one peak.
- Increasing temperature shifts the peak to the left.
- The shift is predicted quantitatively by Wien’s law.
Example (Easy)
A black body has a surface temperature of \( 2900\,\mathrm{K} \). Calculate the wavelength at which it emits maximum radiation.
▶️ Answer / Explanation
\( \lambda_{\text{max}} = \dfrac{2.898\times10^{-3}}{2900} \)
\( \lambda_{\text{max}} \approx 1.0\times10^{-6}\,\mathrm{m} \)
This lies in the infrared region.
Example (Medium)
The peak wavelength of radiation from a star is \( 500\,\mathrm{nm} \). Estimate the surface temperature of the star.
▶️ Answer / Explanation
Convert wavelength to metres:
\( 500\,\mathrm{nm} = 5.0\times10^{-7}\,\mathrm{m} \)
Use Wien’s law:
\( T = \dfrac{2.898\times10^{-3}}{5.0\times10^{-7}} \)
\( T \approx 5.8\times10^{3}\,\mathrm{K} \)
Example (Hard)
A black body’s peak wavelength changes from \( 1.2\times10^{-6}\,\mathrm{m} \) to \( 6.0\times10^{-7}\,\mathrm{m} \). By what factor has its temperature changed?
▶️ Answer / Explanation
Using Wien’s law:
\( \dfrac{T_2}{T_1} = \dfrac{\lambda_1}{\lambda_2} \)
\( \dfrac{T_2}{T_1} = \dfrac{1.2\times10^{-6}}{6.0\times10^{-7}} = 2 \)
The temperature has doubled.