Edexcel A Level (IAL) Physics-5.40 Inverse Square Law of Flux- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -5.40 Inverse Square Law of Flux- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -5.40 Inverse Square Law of Flux- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
Intensity, Luminosity and Distance from a Source
The intensity of radiation from a source depends on how much power the source emits and how far away the observer is.
Definition of Luminosity
Luminosity \( L \) is the total power emitted by a source in all directions.
- Measured in watts (W)
- Independent of distance
- Property of the source itself
Definition of Intensity
Intensity \( I \) is the power received per unit area at a given distance from the source.
\( I = \dfrac{L}{4\pi d^2} \)
- \( I \) = intensity (W m⁻²)
- \( L \) = luminosity of the source (W)
- \( d \) = distance from the source (m)
Meaning of the Equation
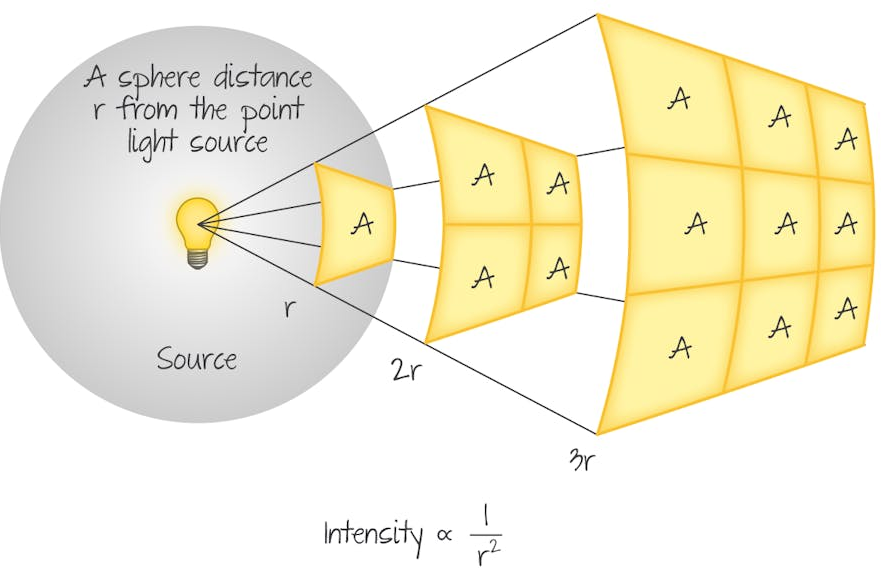
- Radiation spreads out uniformly in all directions.
- At distance \( d \), radiation is spread over a sphere of area \( 4\pi d^2 \).
- As distance increases, intensity decreases.
Key idea:
- Intensity follows an inverse-square law.
Inverse-Square Relationship
- Doubling the distance reduces intensity by a factor of 4.
- Tripling the distance reduces intensity by a factor of 9.
- This applies to light, sound, and radiation from point sources.
Rearranging the Equation
To find luminosity:
\( L = 4\pi d^2 I \)
To find distance:
\( d = \sqrt{\dfrac{L}{4\pi I}} \)
Example (Easy)
A star has luminosity \( 4.0\times10^{26}\,\mathrm{W} \). Calculate the intensity at a distance of \( 2.0\times10^{11}\,\mathrm{m} \).
▶️ Answer / Explanation
\( I = \dfrac{L}{4\pi d^2} \)
\( I = \dfrac{4.0\times10^{26}}{4\pi(2.0\times10^{11})^2} \)
\( I \approx 8.0\times10^{2}\,\mathrm{W\,m^{-2}} \)
Example (Medium)
The intensity of radiation from a star at Earth is \( 1400\,\mathrm{W\,m^{-2}} \). If Earth is \( 1.5\times10^{11}\,\mathrm{m} \) from the star, calculate the luminosity.
▶️ Answer / Explanation
\( L = 4\pi d^2 I \)
\( L = 4\pi(1.5\times10^{11})^2(1400) \)
\( L \approx 3.9\times10^{26}\,\mathrm{W} \)
Example (Hard)
The distance from a star is doubled. By what factor does the intensity of radiation change?
▶️ Answer / Explanation
Using the inverse-square law:
\( I \propto \dfrac{1}{d^2} \)
Doubling \( d \Rightarrow I \) becomes \( \dfrac{1}{4} \) of its original value