Edexcel A Level (IAL) Physics-5.41 Parallax- Study Notes- New Syllabus

Determining Astronomical Distances Using Trigonometric Parallax

Trigonometric parallax is a geometric method used to measure the distances to nearby stars by observing their apparent shift in position.

 What Is Trigonometric Parallax?

As the Earth orbits the Sun, a nearby star appears to shift slightly relative to distant background stars.

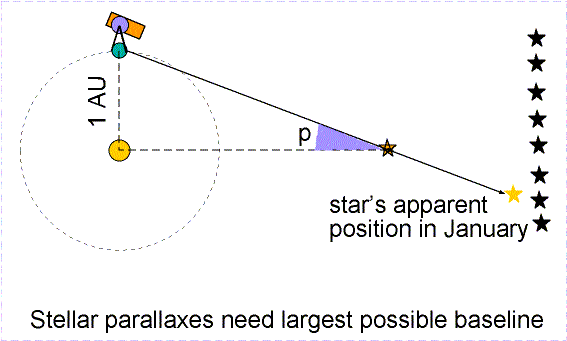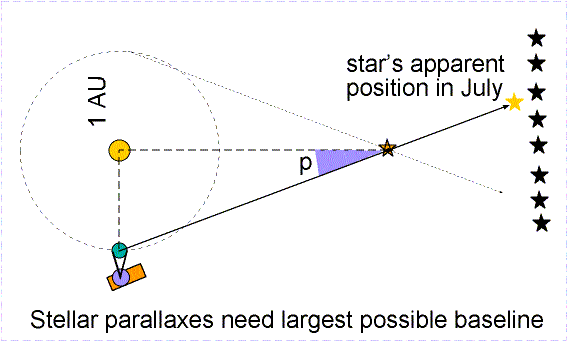
• This apparent shift is called parallax.
• More distant stars show a smaller parallax.
• Nearby stars show a larger parallax.

Key idea:

• Distance is found using geometry and trigonometry.

Parallax Angle

The parallax angle \( p \) is defined as:

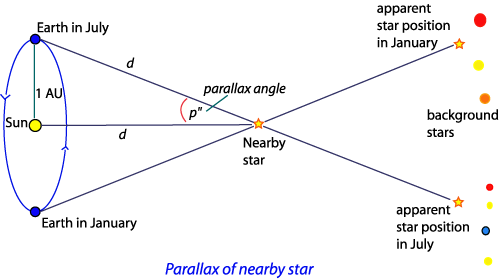
• Half the total angular shift observed over six months.
• The angle subtended at the star by a baseline of 1 astronomical unit (AU).

Baseline:

• Earth–Sun distance = 1 AU

Distance Formula Using Parallax

For very small angles:

\( d = \dfrac{1}{p} \)

• \( d \) = distance to the star (parsecs)
• \( p \) = parallax angle (arcseconds)

Important:

• This formula defines the parsec.
• 1 parsec is the distance at which \( p = 1 \) arcsecond.

Meaning of a Parsec

• 1 parsec ≈ \( 3.09\times10^{16}\,\mathrm{m} \)
• Used for nearby stars.
• Larger distances require other methods.

Limitations of Trigonometric Parallax

• Parallax angles are extremely small.
• Measurement accuracy limits the method.
• Effective only for relatively nearby stars.

Conclusion:

• Best method for stars within a few hundred parsecs.