Edexcel A Level (IAL) Physics-5.46 Equations for Cosmology- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -5.46 Equations for Cosmology- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -5.46 Equations for Cosmology- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
- be able to use the equations for redshift $z = \frac{\Delta \lambda}{\lambda} \approx \frac{\Delta f}{f} \approx \frac{v}{c}$ for a source of electromagnetic radiation moving relative to an observer and $v = H_0 d$ for objects at cosmological distances
Redshift, Doppler Effect and Hubble’s Law
Redshift is observed when electromagnetic radiation from a source moving away from an observer has a longer wavelength and a lower frequency than when it was emitted.
Definition of Redshift
Redshift \( z \) is defined as the fractional change in wavelength:![]()
\( z = \dfrac{\Delta \lambda}{\lambda} \)
- \( \lambda \) = original (emitted) wavelength
- \( \Delta \lambda \) = increase in wavelength
- \( z \) = redshift (dimensionless)
Key idea:
- Redshift occurs when the source is moving away.
- Blueshift occurs when the source is moving towards the observer.
Redshift and Frequency
Since \( c = f\lambda \), a change in wavelength corresponds to a change in frequency.![]()
For small speeds compared to the speed of light:
\( z \approx \dfrac{\Delta f}{f} \)
- Observed frequency decreases for a receding source.
- Observed frequency increases for an approaching source.
Redshift and Recession Speed
For non-relativistic speeds \( (v \ll c) \), redshift is approximately:
\( z \approx \dfrac{v}{c} \)
- \( v \) = recession speed of the source
- \( c \) = speed of light
Important:
- This approximation is valid only for small redshifts.
- Relativistic equations are needed for very distant galaxies.
Hubble’s Law![]()
At cosmological distances, the recession speed of a galaxy is proportional to its distance:
\( v = H_0 d \)
- \( v \) = recession speed (m s⁻¹)
- \( H_0 \) = Hubble constant (s⁻¹)
- \( d \) = distance from Earth (m)
Meaning:
- More distant galaxies move away faster.
- Provides evidence that the Universe is expanding.
Linking Redshift and Distance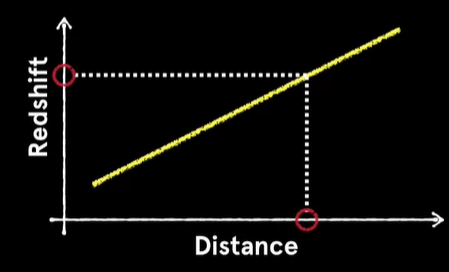
Combining:
- \( z \approx \dfrac{v}{c} \)
- \( v = H_0 d \)
Gives:
\( z \approx \dfrac{H_0 d}{c} \)
This allows astronomers to estimate distances to faraway galaxies.
Example (Easy)
A spectral line is observed at a wavelength \( 660\,\mathrm{nm} \) instead of its emitted wavelength \( 600\,\mathrm{nm} \). Calculate the redshift.
▶️ Answer / Explanation
\( z = \dfrac{\Delta \lambda}{\lambda} = \dfrac{660 – 600}{600} \)
\( z = \dfrac{60}{600} = 0.10 \)
Example (Medium)
A galaxy has a redshift of \( 0.020 \). Estimate its recession speed.
▶️ Answer / Explanation
Use \( z \approx \dfrac{v}{c} \):
\( v = zc = 0.020 \times 3.0\times10^8 \)
\( v = 6.0\times10^6\,\mathrm{m\,s^{-1}} \)
Example (Hard)
A galaxy is \( 3.0\times10^{24}\,\mathrm{m} \) away. Using \( H_0 = 2.2\times10^{-18}\,\mathrm{s^{-1}} \), calculate:
(a) its recession speed (b) its redshift
▶️ Answer / Explanation
(a) Recession speed:
\( v = H_0 d = (2.2\times10^{-18})(3.0\times10^{24}) \)
\( v = 6.6\times10^6\,\mathrm{m\,s^{-1}} \)
(b) Redshift:
\( z \approx \dfrac{v}{c} = \dfrac{6.6\times10^6}{3.0\times10^8} \)
\( z \approx 0.022 \)
