[MAI 4.4] LINEAR REGRESSION-manav-ready
Question
[Maximum mark: 7]
Consider the following data
(a) Find the correlation coefficient r. [1]
(b) Describe the relation between x and y. [2]
(c) Find the equation y = ax+b of the regression line for y on x. [2]
(d) Describe what the coefficient a represents. [1]
(e) Describe what the constant b represents. [1]
▶️Answer/Explanation
Ans:
(a) 0.965
(b) strong positive
(c) y = 2.2x – 0.5
(d) whenever x increases by 1 unit, y increases by 2.2 units.
(e) The value of y corresponding to 0 units of x.
Question
[Maximum mark: 6]
Consider the following data
The regression line for y on x is y = 2.2x – 0.5
(a) Solve the equation above for x to find an expression in the form x = ay+b [2]
(b) Find the equation x = cy+d of the regression line for x on y. [2]
(c) Describe the advantage of the linear equation in (b). [2]
▶️Answer/Explanation
Ans:
(a) y = 2.2x – 0.5 ⇔ y + 0.5 = 2.2x ⇔ x = 0.455 y + 0.227
(b) x = 0.423y + 0.385
(c) The relation in (a) is in fact the inverse function of the line y = 2.2x – 0.5
If y is given, the answer in (c) gives a more reliable estimation of x.
Question
[Maximum mark: 4]
Consider the following data
(a) Find Spearman’s rank correlation coefficient rs. [2]
(b) Describe the meaning of this coefficient. [2]
▶️Answer/Explanation
Ans:
(a) rs = 1.
(b) It describes the monotonic relationship of the data. When x increases y also increases.
Question
[Maximum mark: 4]
Statements I, II, III, IV and V represent descriptions of the correlation between two variables.
I High positive linear correlation
II Low positive linear correlation
III No correlation
IV Low negative linear correlation
V High negative linear correlation
Which statement best represents the relationship between the two variables shown in each of the scatter diagrams below.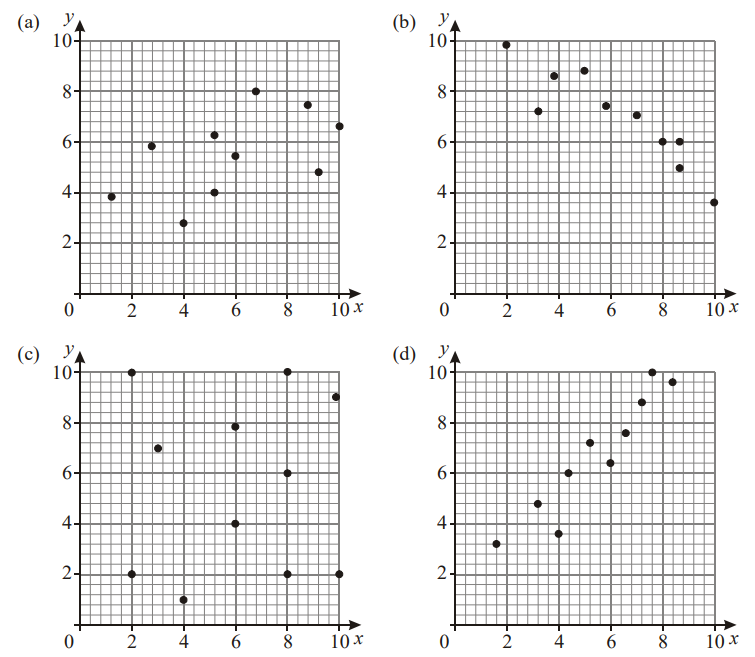
▶️Answer/Explanation
Ans:
(a) II
(b) V
(c) III
(d) I
Question
[Maximum mark: 7]
The sketches below represent scatter diagrams for the way in which variables x, y and z change over time, t, in a given chemical experiment.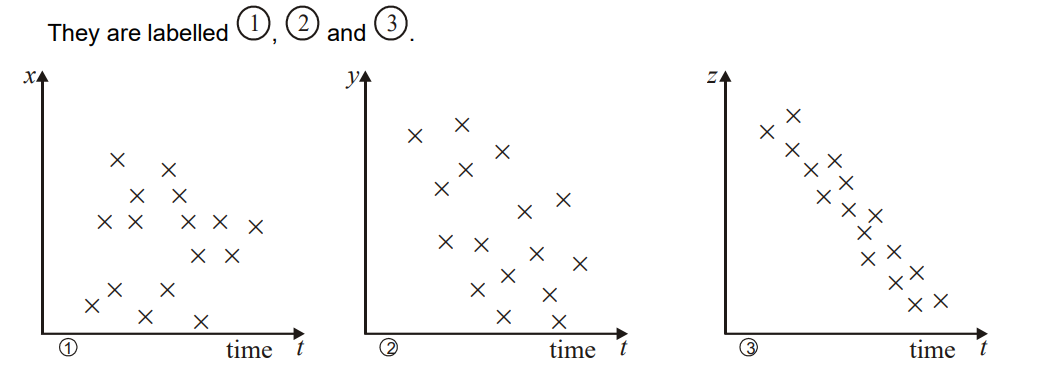
(a) State which of the diagrams indicate that the pair of variables
(i) is not correlated. (ii) shows strong linear correlation. [2]
(b) A student is given a piece of paper with five numbers written on it. She is told that three of these numbers are the product moment correlation coefficients for the three pairs of variables shown above. The five numbers are
0.9, –0.85, –0.20, 0.04, 1.60
(i) For each sketch above state which of these five numbers is the most appropriate value for the correlation coefficient. [3]
(ii) For the two remaining numbers, state why you reject them for this experiment. [2]
▶️Answer/Explanation
Ans:
(a) (I) 1 (ii) 3
(b) (I) 1 0.04 2 -0.20 3 -0.85
(ii) 1.60 A product–moment correlation coefficient cannot be > 1.
0.90 There is no diagram with a strong positive correlation.
Question
[Maximum mark: 4]
The length and width of 10 leaves are shown on the scatter diagram below.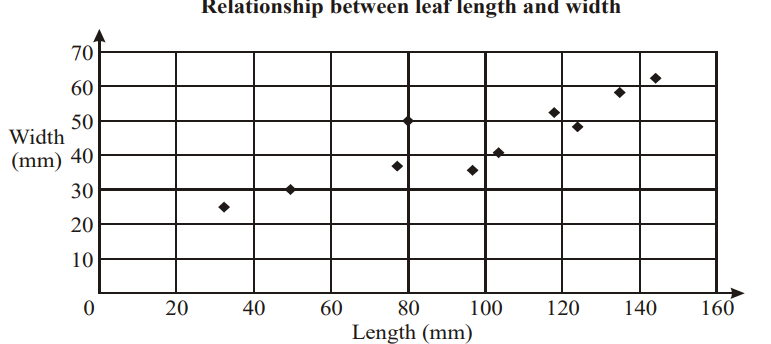
(a) Plot the point M(97, 43) which represents the mean length and the mean width. [1]
(b) Draw a suitable line of best fit. [2]
(c) Write a sentence describing the relationship between leaf length and leaf width for this sample. [1]
▶️Answer/Explanation
Ans:
(a) (see diagram)
(b)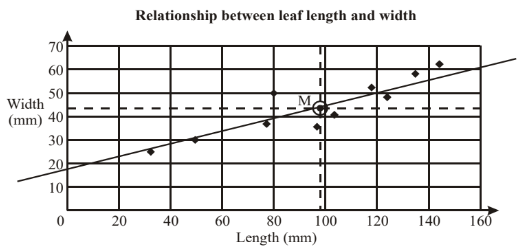
(c) leaf length and leaf width are positively correlated
Question
[Maximum mark: 5]
Ten students were asked for their average grade at the end of their last year of high school and their average grade at the end of their last year at university. The results were put into a table as follows: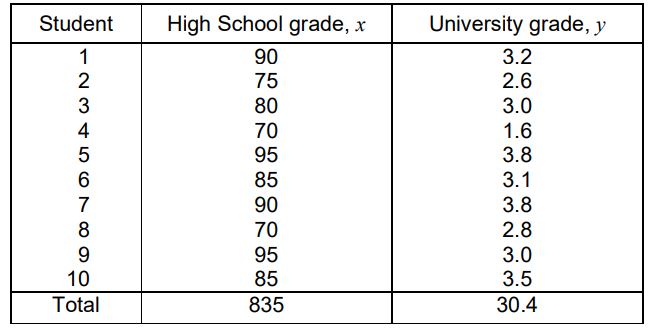
(a) Find the correlation coefficient r. [1]
(b) Describe the correlation between the high school and the university grades. [2]
(c) Find the equation of the regression line for y on x. [2]
▶️Answer/Explanation
Ans:
(a) r = 0.76
(b) Fairly strong positive correlation between high school grades and university grades
(c) y = 0.052x – 1.29 (3 s.f.)
Question
[Maximum mark: 5]
The diagram below shows the marks scored by pupils in a French test and a German test. The mean score on the French test is 29 marks and on the German test is 31 marks.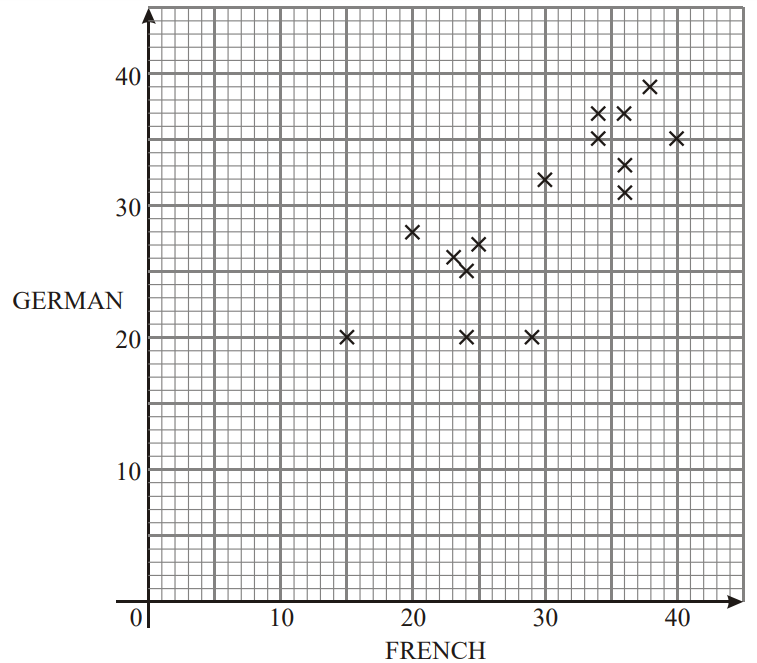
(a) Describe the relationship between the scores. [1]
(b) On the graph mark the point M which represents the mean of the distribution. [1]
(c) Draw a suitable line of best fit. [2]
(d) Idris scored 32 marks on the French test. Use your graph to estimate the mark Idris scored on the German test. [1]
▶️Answer/Explanation
Ans:
(a) High positive or high or positive or good correlation etc.
(b) M(29, 31)
(c) Suitable line which should pass through the candidate’s M and have nearly as many crosses (plotted points) below it as above it.
(d) value (including non-itegers) obtained using candidate’s line of best fit. (Follow through from part (c).)
Question
[Maximum mark: 6]
Eight students in Mr. O’Neil’s Physical Education class did pushups and situps. Their results are shown in the following table.
The graph below shows the results for the first seven students.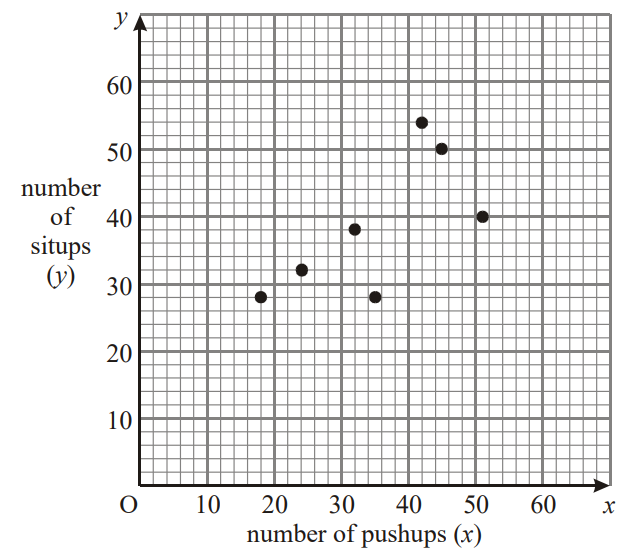
(a) Plot the results for the eighth student on the graph. [1]
(b) Find \(\bar{x}\) and \(\bar{y}\), and draw a line of best fit on the graph. [4]
(c) A student can do 60 pushups. How many situps can the student be expected to do? [1]
▶️Answer/Explanation
Ans:
(a) On the graph
(b) \(\bar{x}=34\) and \(\bar{y}=40\)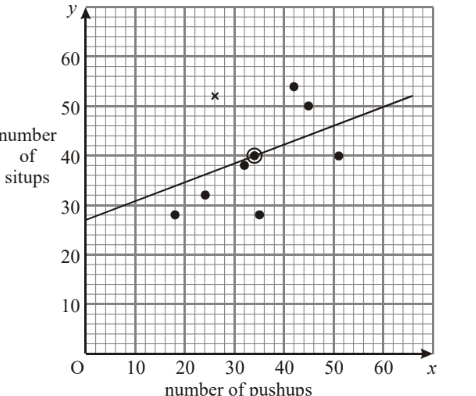
(c) 50 situps (allow ±2) (ft from candidate’s graph)
Question
[Maximum mark: 4]
Ten students were given two tests, one on Mathematics and one on English. The table shows the results of the tests for each of the ten students.
(a) Find correct to two decimal places, the correlation coefficient (r). [2]
(b) Use your result from part (a) to comment on the statement:
‘Those who do well in Mathematics also do well in English. [2]
▶️Answer/Explanation
Ans:
(a) r = 0.6399706… \(\approx\) 0.64 (2 d.p.)
(b) This indicates that there is a degree of positive correlation between scores in Mathematics and scores in English.
Therefore those who do well in Mathematics are likely to do well in English also. (Or equivalent statements.)
Question
[Maximum mark: 6]
The following table contains data for two related variables x and y, and the corresponding ranks for x.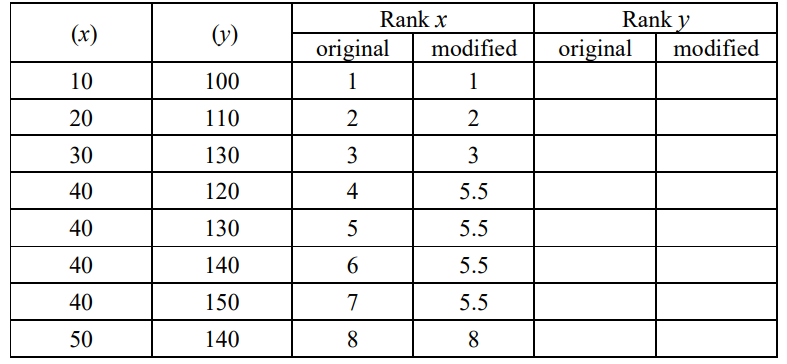
(a) Find the Pearson correlation coefficient r. [2]
(b) Explain how the modified rank 5.5 for the four equal values of x was derived. [1]
(c) Complete the table above; hence find the Spearman rank correlation coefficient. [3]
▶️Answer/Explanation
Ans:
(a) r = 0.838
(b) it is the average of the ranks 4,5,6,7
(c)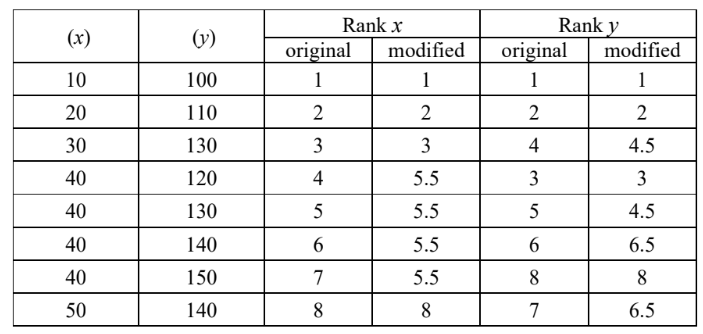
Spearman rank correlation coefficient rs = 0.761
Question
[Maximum mark: 12]
Consider the following data
(a) Find the Pearson correlation coefficient r. [1]
(b) Describe the relation between x and y. [2]
(c) Find the equation y = ax+b of the regression line for y on x. [2]
(d) Find the equation x = cy+d of the regression line for x on y. [2]
(e) Find the Spearman rank correlation coefficient rs [3]
(f) Describe the difference between the two correlation coefficients. [2]
▶️Answer/Explanation
Ans:
(a) r = 0.929
(b) strong positive
(c) y = 0.929 x +10.3
(d) x = 0.929 y – 9
(e) ranks
rs = 0.886
(f) r = 0.929 indicates the degree of linear relationship between x and y (strong positive) rs = 0.886 indicates the degree of monotonic relationship between x and y (in what extent y increases when x increases)
Question
[Maximum mark: 12]
The following table gives the amount of fuel in a car’s fuel tank, and the number of kilometres travelled after filling the tank.
(a) On the scatter diagram below, plot the remaining points. [2]
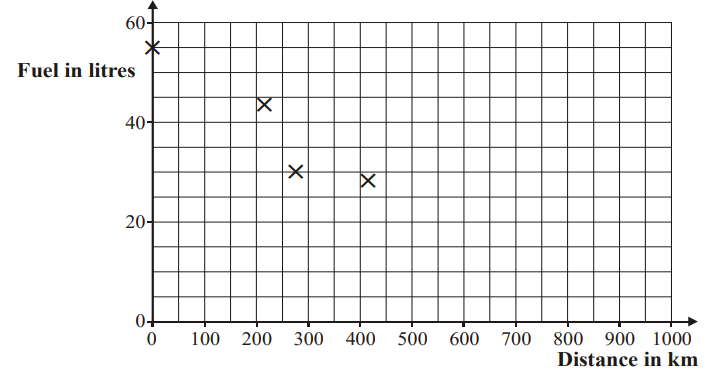
The mean distance travelled is 421 km ( \(\bar{x}\) ), and the mean amount of fuel in the tank is 28 litres ( \(\bar{y}\) ). This point is plotted on the scatter diagram.
(b) Sketch the line of best fit. [3]
(c) A car travelled 350km. Use your line above to estimate the amount of fuel left in the tank. [1]
(d) Find the Pearson correlation coefficient r. [2]
(e) Find the Spearman rank correlation coefficient rs. [2]
(f) Describe the difference between the two correlation coefficients. [2]
▶️Answer/Explanation
Ans:
(a)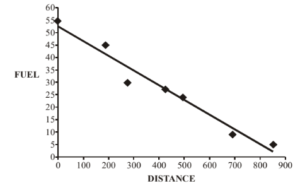
2 marks for all 3 points correct. Only 1 mark for 2 points correct
(b) Straight line with negative gradient passing through the mean intercept on y-axis between 50 and 55
(c) 32 (read answer from candidate’s line)
(d) r = – 0.978
(e) ranks
x 1 2 3 4 5 6
y 6 5 4 3 2 1
rs = –1
(f) r = – 0.978 indicates the degree of linear relationship between x and y (strong negative) rs = –1 indicates a perfect negative monotonic relationship between x and y (y decreases when x increases)
Question
[Maximum mark: 12]
The following table gives the heights and weights of five sixteen-year-old boys.
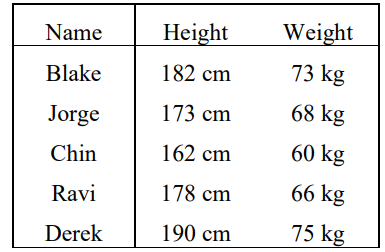
(a) Find (i) the mean height; (ii) the mean weight. [2]
(b) Plot the above data on the grid below and draw the line of best fit. [4]
(c) Find the Pearson correlation coefficient r. [2]
(d) Find the Spearman rank correlation coefficient rs [3]
(e) Explain why rs is not 1. [1]
▶️Answer/Explanation
Ans:
(a) (i) \(\frac{182+173+162+178+190}{5}=177 \mathrm{~cm}\)
(ii) \(\frac{73+68+60+66+75}{5}=68.4 \mathrm{~kg}\) (Or directly by GDC)
(b)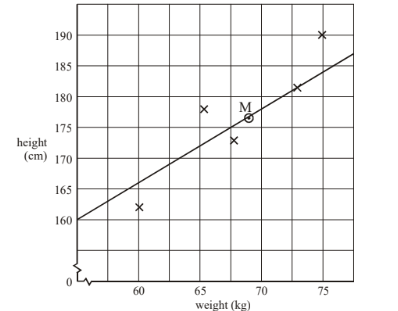
(c) r = 0.943
(d) ranks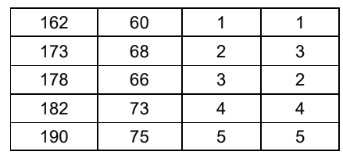
\(r_{S}=0.9\)
(e) Because the rank of y for 173 is larger than the rank of y for 178 (no perfect monotonic relationship)
Question
[Maximum mark: 10]
It is decided to take a random sample of 10 students to see if there is any linear relationship between height and shoe size. The results are given in the table below.
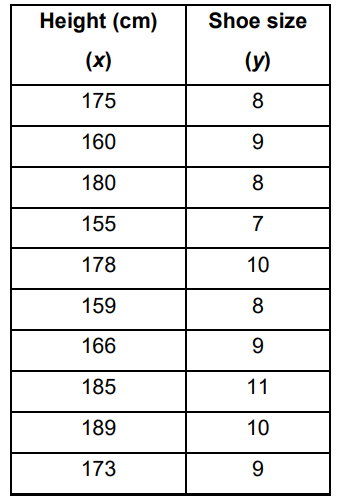
(a) Write down the equation of the regression line of shoe size (y) on height (x),
giving your answer in the form y = mx + c. [2]
(b) State an interpretation for the coefficient m of the regression line in (a). [2]
(c) A student is is 162 cm in height
(i) Use your equation in part (a) to predict the shoe size of the student.
(ii) Is this an interpolation or extrapolation? Explain. [3]
(d) Write down the correlation coefficient. [1]
(e) Describe the correlation between height and shoe size. [2]
▶️Answer/Explanation
Ans:
(a) y = 0.070x – 3.22
Accept 0.07x.
(b) for each cm of height the shoe size increases by 0.070
(c) (i) y = 0.070 × 162 – 3.22 = 8.12
Therefore shoe size 8 or 9 (8.12).
OR y = 8 or 9
(ii) interpolation since a.62 is within the range of values of x.
(d) r = 0.681
(e) Moderately strong, positive correlation.
Question
[Maximum mark: 12]
The heights and weights of 10 students selected at random are shown below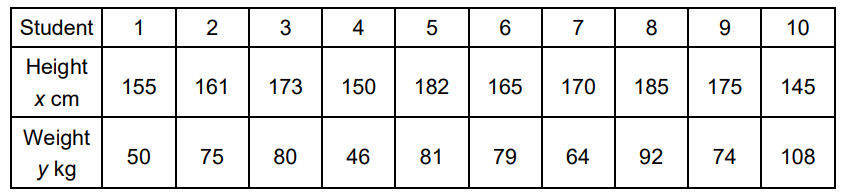
(a) Plot this information on a scatter graph. Use a scale of 1 cm to represent 20 cm on the x-axis and 1 cm to represent 10 kg on the y-axis. [4]
(b) Calculate the mean height and the mean weight [2]
(c) (i) Find the equation of the line of best fit.
(ii) Draw the line of best fit on your graph. [3]
(d) Use your line to estimate
(i) the weight of a student of height 190 cm;
(ii) the height of a student of weight 72 kg. [2]
(e) It is decided to remove the data for student number 10 from all calculations.
Explain briefly what effect this will have on the line of best fit. [1]
▶️Answer/Explanation
Ans:
(a)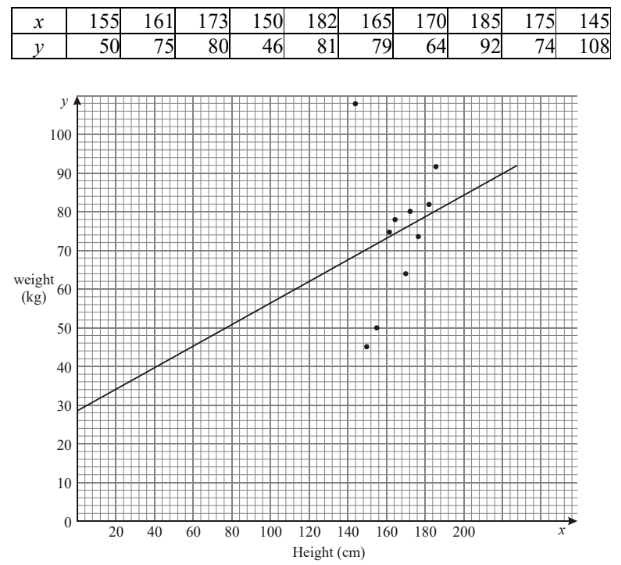
(b) Mean height = 166.1 = 166 (3 s.f.)
Mean weight = 74.9 (3 s.f.)
(c) (i) y = 0.276x + 29.1
(ii) Line on graph. y-intercept at 29.1, straight line through (166, 74.9).
(d) (i) y = 0.276 × 190 + 29.1= 81.5 kg
(ii) 72 = 0.276x + 29.1
\(x=\frac{72-29.1}{0.276}=155 \mathrm{~cm}\)
OR From the graph
(i) y = 81 (\(\pm\)1)
(ii) x = 155 (\(\pm\)1)
(e) The ‘line of best fit’ becomes closer to the remaining points.
OR
Gradient becomes steeper and the line is more accurate ‘best fit’.
OR
Any reasonable explanation. (Line becomes y = 1.10x – 113)
Question
[Maximum mark: 12]
The Type Fast secretarial training agency has a new computer software spreadsheet package. The agency investigates the number of hours it takes people of varying ages to reach a level of proficiency using this package. Fifteen individuals are tested and the results are summarised in the table below.
(a) (i) Find the correlation coefficient r for this data.
(ii) What does the value of the correlation coefficient suggest about the relationship between the two variables? [2]
(b) Write down the equation of the regression line for y on x in the form y = ax + b. [2]
(c) Use your equation for the regression line to predict
(i) the time that it would take a 30 year old person to reach proficiency, giving your answer correct to the nearest hour;
(ii) the age of a person who would take 8 hours to reach proficiency, giving your answer correct to the nearest year. [4]
(d) Find an estimation for the age of the person in question (c)( ii) by using the regression line of x on y. [4]
▶️Answer/Explanation
Ans:
(a) (i) 1992 mean = $1.59, Sd = $0.727 (or 0.73)
(ii) 2002 mean = $1.98, Sd = $0.635 (or 0.64)
(b) (i) r = 0.672
(ii) There is a weak positive correlation
(c) y = 0.588x + 1.05
(d) y = 0.588 × 2.60 + 1.05 = $2.58
(e) Coffee – because it is the only item to go down in price.
OR
Rolls – because the price increased significantly.
Question
[Maximum mark: 12]
A shopkeeper wanted to investigate whether or not there was a correlation between the prices of food 10 years ago in 1992, with their prices today. He chose 8 everyday items and the prices are given in the table below.
(a) Calculate the mean and the standard deviation of the prices
(i) in 1992;
(ii) in 2002. [4]
(b) (i) Find the correlation coefficient.
(ii) Comment on the relationship between the prices. [3]
(c) Find the equation of the line of the best fit in the form y = mx + c. [2]
(d) What would you expect to pay now for an item costing $2.60 in 1992? [1]
(e) Which item would you omit to increase the correlation coefficient? [2]
▶️Answer/Explanation
Ans
Question
[Maximum mark: 12]
The following are the results of a survey of the scores of 10 people on both a mathematics (x) and a science (y) aptitude test: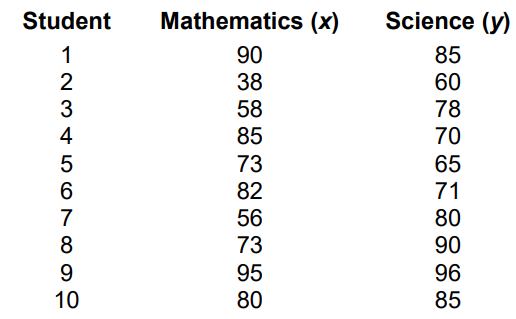
(a) Plot this information on a scatter graph. Use a scale of 1 cm to represent 10 units on the x-axis and 1 cm to represent 10 units on the y-axis. [4]
(b) Find and plot the point M (\(\bar{x}, \bar{y}\)) on the graph. [2]
(c) Find the equation of the regression line of y on x in the form y = ax + b. [2]
(d) Graph this line on the above graph. [2]
(e) Given that a student receives an 88 on the mathematics test, what would you expect this student’s science score to be? Show how you arrived at your result. [2]
▶️Answer/Explanation
Ans:
(a)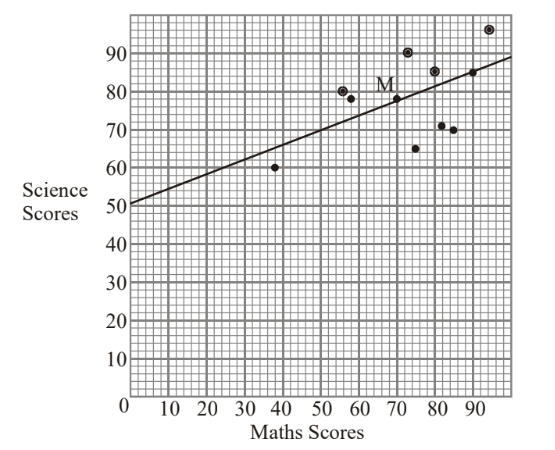
(b) Point M(73,78)
(c) y = 0.359x + 51.8
(d) going through M, y intercept anywhere from 50 to 54
(e) y = 0.359 × 88 + 51.8 = 83
OR
y = 83 (±2) if read from the graph and method is shown.
Question
[Maximum mark: 11]
The following are the results of a survey of the scores of 10 people on both a mathematics (x) and a science (y) aptitude test: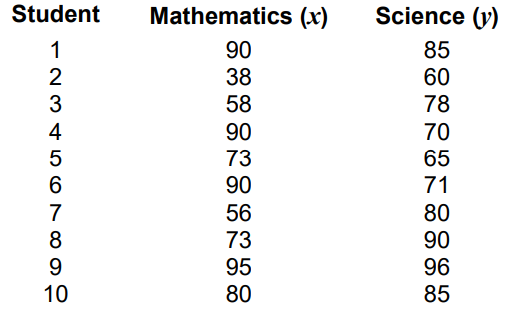
(a) Find the equation of the regression line of y on x. [2]
(b) Find the equation of the regression line of x on y. [2]
(c) Find the Pearson correlation coefficient r. [2]
The table below shows the data for x in increasing order and the corresponding ranks.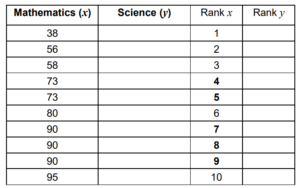
(d) (i) Complete the data for y and the corresponding ranks in the table above.
(ii) Hence, find the Spearman rank correlation coefficient rs [5]
▶️Answer/Explanation
Ans