IBDP Chemistry Reactivity 1.3 Energy from fuels HL Paper 2- Exam Style Questions - New Syllabus

(a)
For the reaction \( \mathrm{CO(g) + H_2O(g) \rightleftharpoons CO_2(g) + H_2(g)} \), the equilibrium constant expression is
\( \boxed{K = \dfrac{[\mathrm{CO_2}][\mathrm{H_2}]}{[\mathrm{CO}][\mathrm{H_2O}]}} \).

(b)
From the stoichiometry of the reaction, formation of \(1.5\,\text{mol}\) of \(\mathrm{CO_2}\) produces \(1.5\,\text{mol}\) of \(\mathrm{H_2}\).

Amounts at equilibrium:
\( n(\mathrm{CO}) = 2.7 – 1.5 = 1.2\,\text{mol} \)
\( n(\mathrm{H_2O}) = 2.9 – 1.5 = 1.4\,\text{mol} \)
\( n(\mathrm{H_2}) = 1.5\,\text{mol} \)

Since the volume is \(1\,\text{dm}^3\), concentrations are numerically equal to the amounts in moles.

\( K = \dfrac{(1.5)(1.5)}{(1.2)(1.4)} = \dfrac{2.25}{1.68} \approx 1.34 \)
\( \boxed{K \approx 1.3} \)

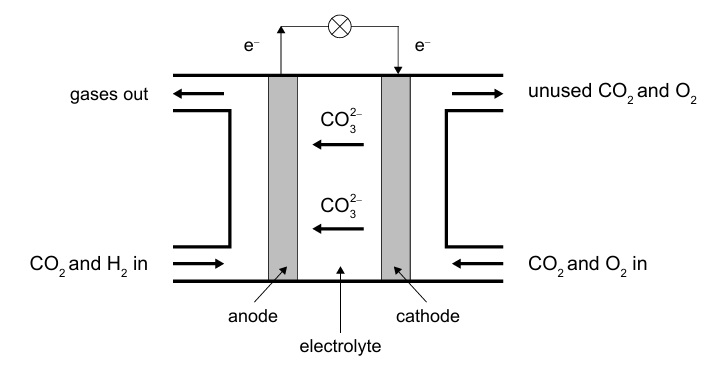
(c)
Anode (oxidation):
\( \mathrm{H_2 + CO_3^{2-} \rightarrow CO_2 + H_2O + 2e^-} \)
Cathode (reduction):
\( \mathrm{CO_2 + \tfrac{1}{2}O_2 + 2e^- \rightarrow CO_3^{2-}} \)

(d)
A molten carbonate fuel cell is environmentally friendly because carbon dioxide produced at the anode can be reused at the cathode, resulting in no net increase in atmospheric carbon dioxide.
\( \boxed{\text{No net } \mathrm{CO_2} \text{ emissions}} \)