IB DP Chemistry -Reactivity 2.2 How fast? The rate of chemical change - IB Style Questions For HL Paper 1A -FA 2025

Question

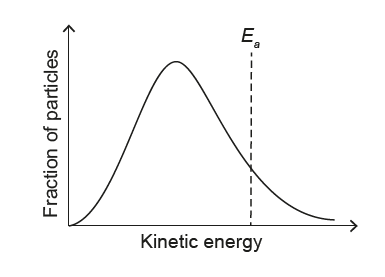
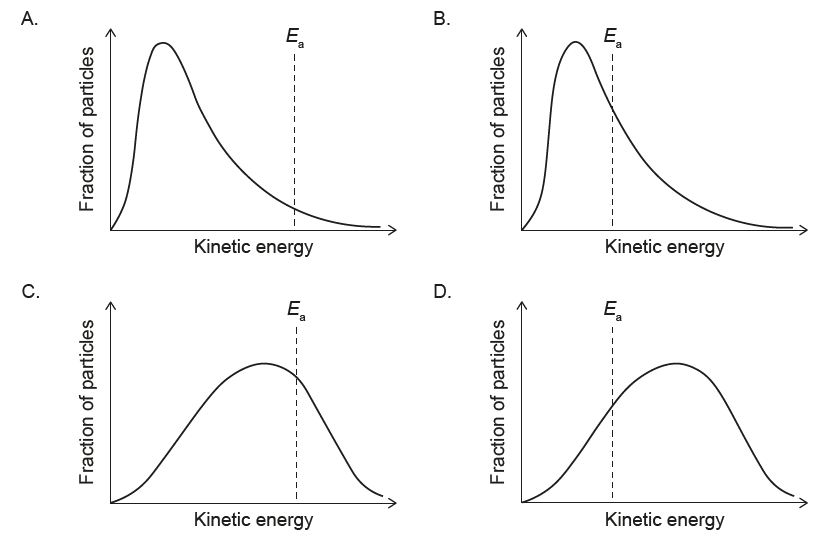
Consider the Maxwell–Boltzmann energy distribution.

Which curve represents the distribution at a lower temperature?

▶️ Answer/Explanation

Detailed solution

At lower T:
• Peak shifts to lower energy (left)
• Peak becomes higher and narrower
• Activation energy E_a is independent of T

✅ Answer: (A)

What happens to the average kinetic energy, KE, of the particles in a gas when the absolute temperature is doubled?

The kinetic energy of a particle is given by:
\[ KE = \frac{1}{2}mv^2 \]

(A) increases by a factor of \(2\)
(B) decreases by a factor of \(2\)
(C) increases by a factor of \(4\)
(D) decreases by a factor of \(4\)

▶️ Answer/Explanation

Detailed solution

Markscheme: A

According to kinetic theory, the average kinetic energy of gas particles is directly proportional to the absolute temperature:

\[ KE = \frac{3}{2}kT \]

where:
\(KE\) = average kinetic energy
\(k\) = Boltzmann constant
\(T\) = absolute temperature

If the absolute temperature increases from \(T\) to \(2T\), then:

\[ KE_2 = \frac{3}{2}k(2T) = 2 \left( \frac{3}{2}kT \right) = 2KE_1 \]

So, when the absolute temperature is doubled, the average kinetic energy also doubles.

✅ Answer: (A)

Which calculation determines the initial rate of this reaction?

(A) \( \dfrac{0.40 – 0.19}{20 – 0} \)
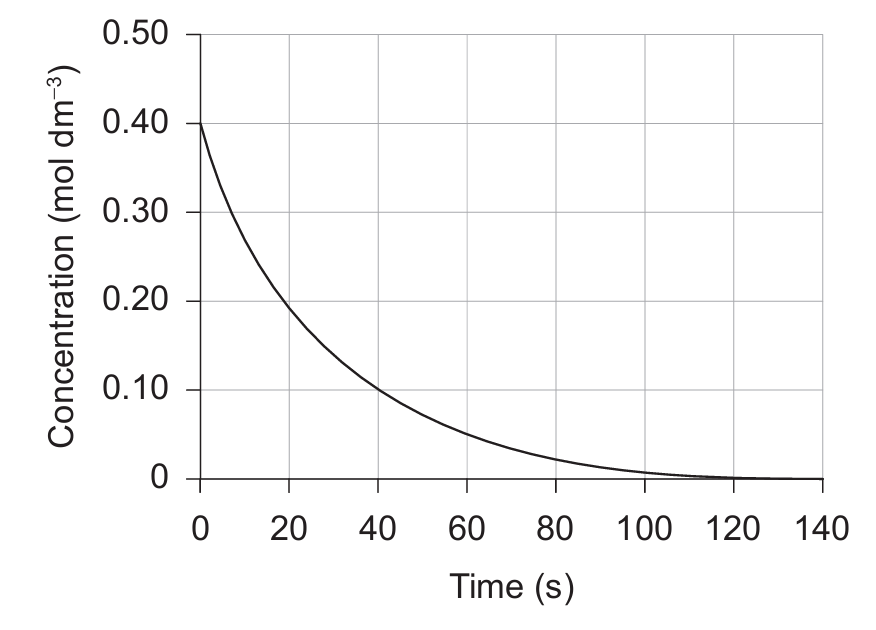
(B) \( \dfrac{0.40 – 0.10}{40 – 0} \)
(C) \( \dfrac{0.40 – 0}{140 – 0} \)
(D) \( \dfrac{0.40 – 0.20}{10 – 0} \)

▶️ Answer/Explanation

Detailed solution

Markscheme: (D)

The rate of reaction can be found using:

\[ \text{rate} = -\frac{\Delta[\text{reactant}]}{\Delta t} \quad \text{or} \quad \text{rate} = \frac{\Delta[\text{product}]}{\Delta t} \]

For the initial rate, we draw a tangent to the graph at \(t = 0\).

From the tangent, the slope can be approximated by:

\[ \frac{0.40 – 0.20}{10 – 0} \quad \text{or} \quad \frac{0.40 – 0.00}{20 – 0} \]

Both expressions simplify to the same initial rate. The closest matching option is:

✅ Answer: (D)