IB DP Chemistry - Structure 1.5 Ideal gases - IB Style Questions For HL Paper 1A -FA 2025
Question
| Gas | Pressure | Temperature |
|---|---|---|
| A. Phosphine, PH3 | Low | High |
| B. Ammonia, NH3 | Low | High |
| C. Phosphine, PH3 | High | Low |
| D. Ammonia, NH3 | High | Low |
▶️ Answer/Explanation
Gases behave most ideally under:
- Low pressure (molecules far apart, negligible intermolecular forces)
- High temperature (high kinetic energy overcomes intermolecular forces)
- Smaller, non-polar molecules deviate less than larger, polar molecules
- PH3 is less polar than NH3
✅ Answer: (A) – PH3 at low pressure and high temperature
Question
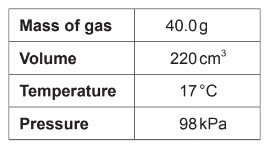
(B) \(\frac{98 \times 0.220}{40.0 \times 8.31 \times 290}\)
(C) \(\frac{40.0 \times 8.31 \times 17}{98 \times 0.220}\)
(D) \(\frac{98 \times 220}{40.0 \times 8.31 \times 17}\)
▶️ Answer/Explanation
To calculate the molar mass of the gas, we start with the ideal gas law:
\[\mathrm{PV = nRT}\]
Rearranging to find the number of moles:
\[\mathrm{n = \frac{PV}{RT}}\]
Substituting the given values:
\[\mathrm{n = \frac{(98 \, kPa)(0.220 \, L)}{(8.31)(290\, K)}}\]
The molar mass \(M\) is then:
\[\mathrm{M = \frac{mass}{moles} = \frac{40.0}{n}}\]
Substituting the value of \(n\) gives:
\[\mathrm{M = \frac{40.0 \times 8.31 \times 290}{98 \times 0.220}}\]
Therefore:
✅ Answer: (A)
Question
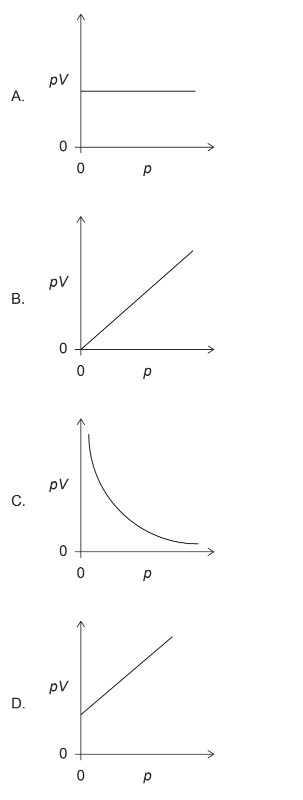
▶️ Answer/Explanation
For a fixed mass of an ideal gas at constant temperature, Boyle’s Law states that:
\[ pV = \text{constant} \]
Since the product \(pV\) is constant, its value does not change as \(p\) changes. Therefore, a graph of \(pV\) (vertical axis) against \(p\) (horizontal axis) must be a horizontal line.
Among the given graphs, the only one that shows a constant value of \(pV\) as \(p\) increases is option (A).
✅ Answer: (A)
