Question
The array DATA_ARR[] is a one-dimensional array of 12 integers.

Algorithm 1 represents a method of searching the array DATA_ARR [ ] to see if it contains a specific value.
Algorithm 1
input TO_FIND
LIMIT = 11
LOC = FALSE
ITERATE $=0$
loop while not LOC and ITERATE <= LIMIT
$\quad$ if DATA_ARR[ITERATE $]=$ TO_FIND then
$\quad$ LOC = TRUE
$\quad$ end if
ITERATE = ITERATE + 1
end loop
if LOC then
output TO_FIND, “is in the array”
else
output TO_FIND, “is NOT in the array”
end if
Algorithm 2 represents an alternative method of searching the array DATA_ARR[] to see if it contains a specific value.
Algorithm 2
input TO_FIND
LOC = FALSE
LOW_LIM = 0
UP_LIM = 11
loop while LOW_LIM <= UP_LIM and LOC = FALSE
MID_VAL = (LOW_LIM + UP_LIM) div 2
if DATA_ARR[MID_VAL] = TO_FIND then
LOC = TRUE
else
if TO_FIND < DATA_ARR[MID_VAL] then
UP_LIM = MID_VAL – 1
else
LOW_LIM = MID_VAL + 1
end if
end if
end loop
if LOC = TRUE then
output TO_FIND, “is in the array”
else
output TO_FIND, “is NOT in the array”
end if
a.)Copy and complete the trace table for Algorithm 1 using TO_FIND = 39.[4]
The first value of the first row has been done for you.

b. State the constant used in Algorithm 1. [1]
c. Copy and complete the trace table for Algorithm 2 using TO_FIND $=50$.[4]
The first two values of the first row have been done for you.

d. Outline why MID_VAL could not be a constant. [1]
e. Evaluate the use of a sequential search and a binary search including the advantages and disadvantages of each. [5]
▶️Answer/Explanation
Ans:
a. )
Award [1] for TO_FIND and Loc columns;
Award [1] for ITERATE column;
Award [1] for DATA_ARR [ITERATE] column;
Award [1] for the correct output;
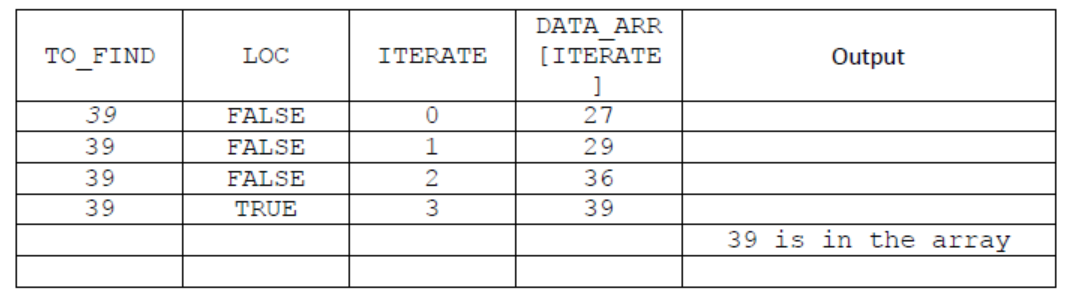
b. )
LIMIT
c. )
Award [1] for Low_LIM column;
Award [1] for UP_LIM column;
Award [1] for MID_VAL and DATA_ARR [MID_VAL] columns;
Award [1] for TO_FIND, LOC and Output columns;
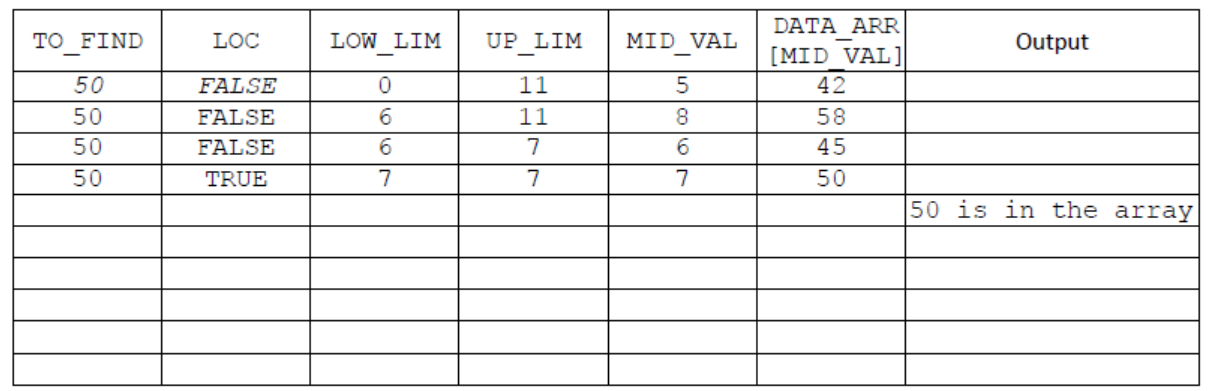
d.)
The value (of MID_VAL) changes during the operation of the algorithm;
e.)
The algorithm searches through every element in the array starting at the beginning and working through one after the other; … until the required item is found;
This method is potentially slow if the data set is large and the required element is towards the end of the list; The data does not need to be in any particular order;
Award $[3$ max] for binary search
The data must be sorted before it is stored;
After comparing the data set with the target data, half of the data can be discounted using a simple condition; …enabling the target to be more quickly located;
Note to examiners: Big O notation is not on the syllabus so answers with reference to this are not expected, however, if this type of answer is seen, please allow, for example:
Sequential: main disadvantage is $\mathrm{O}(\mathrm{N})$ so inefficient; advantage is that it works with an unsorted array;
Binary search: main advantage is that it’s efficient as it’s $O(\log n)$;
disadvantage is that the array must be sorted (and so must be sortable – not all data has a defined sort order);
Binary search cannot be performed on a linked list but a sequential search can;
Question
Outline the need for a translation process from high level language to machine code.
▶️Answer/Explanation
Ans:
(The program written in HLL must be translated into machine code) so that the computer can execute the program; as the computer only understands machine language / as code written in HLL can only be understood by humans and cannot be interpreted by the computers (which work in binary);
Question
A school teacher decides to write a program to store class records and marks. Part of this program involves using a sort algorithm. The algorithm shown is a selection sort and to test it, the teacher has set up an array VALUES[] with 5 elements of test data.
LIMIT = 4
loop COUNTER1 from 0 to LIMIT – 1
MINIMUM = COUNTER1
loop COUNTER2 from COUNTER1 + 1 to LIMIT
if VALUES[COUNTER2] < VALUES[MINIMUM] then
MINIMUM = COUNTER2
end if
end loop
if MINIMUM ≠ COUNTER1 then
TEMPORARY = VALUES[MINIMUM]
VALUES[MINIMUM] = VALUES[COUNTER1]
VALUES[COUNTER1] = TEMPORARY
end if
end loop
a.)Copy and complete the table below to trace the algorithm using the data set:[5]
20, 6, 38, 50, 40
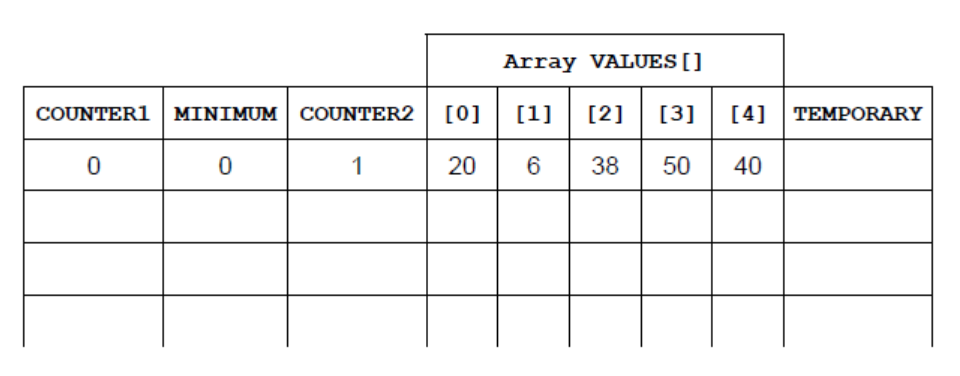
b.i. With reference to the algorithm in the flow chart, construct this algorithm in pseudocode so that it performs the same function.[3]
b.ii.State the type of sort in the algorithm constructed in b(i).[1]
c. Construct an algorithm fragment to output the data in the array vALUES [ ] [2]
▶️Answer/Explanation
Ans:
a.)
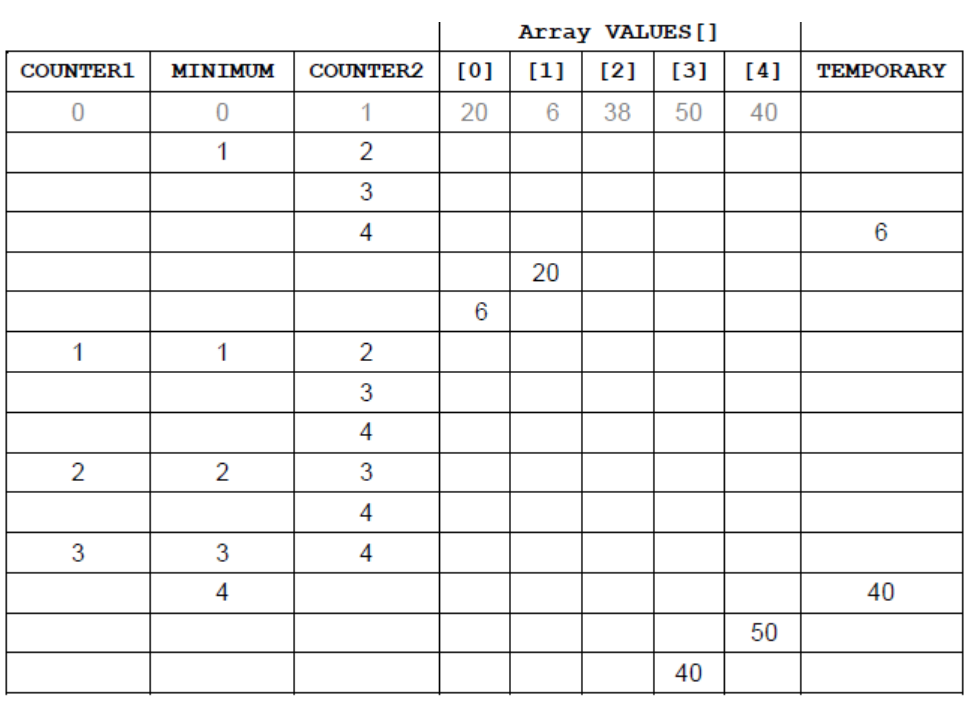
Both COUNTER1 and COUNTER2 correct;
MINIMUM column correct;
Final VALUES[] 0, 1, 2 correct;
Final VALUES[] 3, 4 correct;
TEMPORARY column correct;
Note to examiners:
Allow follow through (FT).
In case of different representation of values in columns COUNTER1 and COUNTER2, then FT, award marks for the correct values of the variables MINIMUM and TEMPORARY.
b.)
Use of correct nested loops;
Correct use of flag;
Inner loop checking adjacent cells;
Values being swapped if necessary;
Example algorithm 1:
LIMIT = 4
FLAG = TRUE
loop while FLAG = TRUE
FLAG = FALSE
loop COUNTER from 0 to LIMIT – 1
if VALUES[COUNTER] > VALUES[COUNTER + 1] then
TEMPORARY = VALUES[COUNTER]
VALUES[COUNTER] = VALUES[COUNTER + 1]
VALUES[COUNTER + 1] = TEMPORARY
FLAG = TRUE
end if
end loop
end loop
A recursive solution is allowed at HL. SL candidates who submit an above level recursive solution should also receive credit.
Version 1 – basic recursive solution
BUBBLESORT defined as a procedure with correct pass through parameters and end/return statement;
Correct loop with values swapped if necessary inside procedure;
Recursive call of BUBBLESORT with parameters passed;
Correct condition for recursive call;
Example algorithm 2
LIMIT = 4
BUBBLESORT(VALUES, LIMIT)
loop COUNTER from 0 to LIMIT – 1
if VALUES[COUNTER] > VALUES[COUNTER + 1] then
TEMPORARY = VALUES[COUNTER]
VALUES[COUNTER] = VALUES[COUNTER + 1]
VALUES[COUNTER + 1] = TEMPORARY
end if
end loop
if LIMIT – 1 > 1 then
call BUBBLESORT(VALUES, LIMIT – 1)
end if
end BUBBLESORT
Version 2 – more efficient recursive solution
BUBBLESORT defined as a procedure with correct pass through
parameters and end/return statement;
Correct loop with values swapped if necessary inside procedure;
Recursive call of BUBBLESORT with parameters passed;
Correct condition for recursive call;
Correct use of flag;
Example algorithm 2
LIMIT = 4
BUBBLESORT(VALUES, LIMIT)
FLAG = FALSE
loop COUNTER from 0 to LIMIT – 1
if VALUES[COUNTER] > VALUES[COUNTER + 1] then
TEMPORARY = VALUES[COUNTER]
VALUES[COUNTER] = VALUES[COUNTER + 1]
VALUES[COUNTER + 1] = TEMPORARY
FLAG = TRUE
end if
end loop
if LIMIT – 1 > 1 and FLAG = TRUE then
call BUBBLESORT(VALUES, LIMIT – 1)
end if
end BUBBLESORT
b.ii.)
Bubblesort;
c)
Use of (any type of) loop;
Correct output statement;
Example algorithm:
loop COUNTER from 0 to LIMIT
output VALUES[COUNTER]
end loop
