Question: [Maximum mark: 8]
Consider \(\lim_{x\rightarrow 0}\frac{arctan(cosx)-k}{x^{2}},\) where k ∈ R.
(a) Show that a finite limit only exists for k = \(\frac{\pi }{4}\).
(b) Using l’Hôpital’s rule, show algebraically that the value of the limit is \(-\frac{1}{4}\).
▶️Answer/Explanation
Ans:
(a) (as \(\lim_{x\rightarrow 0}x^{2} = 0,\) the indeterminate form \(\frac{0}{0}\) s required for the limit to exist)
\(\Rightarrow \lim_{x\rightarrow 0}\left ( arctan(cosx)-k \right )=0\)
arctan1 – k = 0 (k = arctan1)
so \(k = \frac{\pi }{4}\)
Note: Award M1A0 for using \(k = \frac{\pi }{4}\) to show the limit is \(\frac{0}{0}\).
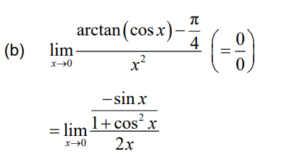
Note: Award A1 for a correct numerator and A1 for a correct denominator.
recognises to apply l’Hôpital’s rule again
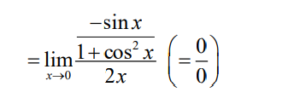
Note: Award M0 if their limit is not the indeterminate form \(\frac{0}{0}\).
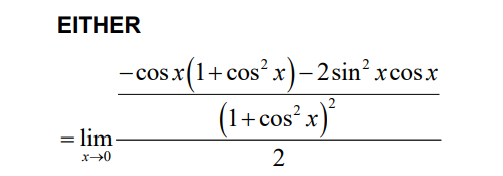
Note: Award A1 for a correct first term in the numerator and A1 for a correct second term in the numerator.
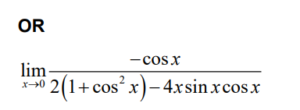
Note: Award A1 for a correct numerator and A1 for a correct denominator.
THEN
substitutes x = 0 into the correct expression to evaluate the limit
Note: The final A1 is dependent on all previous marks.
\(-\frac{1}{4}\)
Question
Use l’Hôpital’s rule to find
\(lim_{x\rightarrow 1}\frac{cos(x^2-1)-1}{e^{x-1}-x}\)
▶️Answer/Explanation
Ans:
attempt to use l’Hôpital’s rule
= \(lim_{x\rightarrow 1}\frac{-2xsin(x^{2}-1)}{e^{x-1}-1}\)
Note: Award A1 for the numerator and A1 for the denominator.
substitution of 1 into their expression =\( _{0}^{0}\)hence use l’Hôpital’s rule again
Note: If the first use of l’Hôpital’s rule results in an expression which is not in indeterminate form, do not award any further marks.
attempt to use product rule in numerator
= \(lim_{x\rightarrow 1}\frac{-4x^{2}cos(x^{2}-1)-2 sin (x^{2}-1)}{e^{x-1}}=-4\)
Question
(a) (i) Using l’Hôpital’s rule, show that
\[\mathop {\lim }\limits_{x \to \infty } \frac{{{x^n}}}{{{{\text{e}}^{\lambda x}}}} = 0;{\text{ }}n \in {\mathbb{Z}^ + },{\text{ }}\lambda \in {\mathbb{R}^ + }\]
(ii) Using mathematical induction on \(n\), prove that
\[\int_0^\infty {{x^n}{{\text{e}}^{ – \lambda x}}{\text{d}}x = \frac{{n!}}{{{\lambda ^{n + 1}}}};{\text{ }}} n \in \mathbb{N},{\text{ }}\lambda \in {\mathbb{R}^ + }\]
(b) The random variable \(X\) has probability density function
\[f(x) = \left\{ \begin{array}{l}\frac{{{\lambda ^{n + 1}}{x^n}{{\rm{e}}^{ – \lambda x}}}}{{n!}}x \ge 0,n \in {\mathbb{Z}^ + },\lambda \in {\mathbb{R}^ + }\\{\rm{otherwise}}\end{array} \right.\]
Giving your answers in terms of \(n\) and \(\lambda \), determine
(i) \({\text{E}}(X)\);
(ii) the mode of \(X\).
(c) Customers arrive at a shop such that the number of arrivals in any interval of duration \(d\) hours follows a Poisson distribution with mean \(8d\). The third customer on a particular day arrives \(T\) hours after the shop opens.
(i) Show that \({\text{P}}(T > t) = {{\text{e}}^{ – 8t}}\left( {1 + 8t + 32{t^2}} \right)\).
(ii) Find an expression for the probability density function of \(T\).
(iii) Deduce the mean and the mode of \(T\).
▶️Answer/Explanation
Markscheme
(a) (i) using l’Hopital’s rule once,
\(\mathop {{\text{lim}}}\limits_{x \to \infty } \frac{{{x^n}}}{{{{\text{e}}^{\lambda x}}}} = \mathop {{\text{lim}}}\limits_{x \to \infty } \frac{{n{x^{n – 1}}}}{{\lambda {{\text{e}}^{\lambda x}}}}\) (A1)(A1)
Note: Award A1 for numerator, A1 for denominator.
if \(n > 1\), this still gives \(\frac{\infty }{\infty }\) so differentiate again giving
\(\mathop {{\text{lim}}}\limits_{x \to \infty } \frac{{n(n – 1){x^{n – 2}}}}{{{\lambda ^2}{{\text{e}}^{\lambda x}}}}\) (A1)
if \(n > 2\), this still gives \(\frac{\infty }{\infty }\) so differentiate a further \(n – 2\) times giving M1
\(\mathop {{\text{lim}}}\limits_{x \to \infty } \frac{{n!}}{{{\lambda ^n}{{\text{e}}^{\lambda x}}}}\) A1
\( = 0\) AG
(ii) first prove the result true for \(n = 0\)
\(\int_0^\infty {{{\text{e}}^{ – \lambda x}}{\text{d}}x = – \frac{1}{\lambda }\left[ {{{\text{e}}^{ – \lambda x}}} \right]_0^\infty = \frac{1}{\lambda }} \) as required M1A1
assume the result is true for \(n = k\) M1
\(\int_0^\infty {{x^k}{{\text{e}}^{ – \lambda x}}{\text{d}}x = \frac{{k!}}{{{\lambda ^{k + 1}}}}} \)
consider, for \(n = k + 1\),
\(\int_0^\infty {{x^{k + 1}}{{\text{e}}^{ – \lambda x}}{\text{d}}x = – \frac{1}{\lambda }\left[ {{x^{k + 1}}{{\text{e}}^{ – \lambda x}}} \right]_0^\infty + \frac{{k + 1}}{\lambda }\int_0^\infty {{x^k}{{\text{e}}^{ – \lambda x}}{\text{d}}x} } \) M1A1
\( = (0 + )\frac{{k + 1}}{\lambda } \times \frac{{k!}}{{{\lambda ^{k + 1}}}}\) A1
\( = \frac{{(k + 1)!}}{{{\lambda ^{k + 2}}}}\) A1
therefore true for \(n = k \Rightarrow \) true for \(n = k + 1\) and since true for \(n = 0\), the result is proved by induction R1
Note: Only award the R1 if at least 4 of the previous marks have been awarded.
Note: If a candidate starts at \(n = 1\), do not award the first 2 marks but follow through thereafter.
[13 marks]
(b) (i) \({\text{E}}(X) = \frac{{{\lambda ^{n + 1}}}}{{n!}}\int_0^\infty {{x^{n + 1}}} {{\text{e}}^{ – \lambda x}}{\text{d}}x\) M1
\( = \frac{{{\lambda ^{n + 1}}}}{{n!}} \times \frac{{(n + 1)!}}{{{\lambda ^{n + 2}}}}\) A1
\( = \frac{{(n + 1)}}{\lambda }\) A1
(ii) the mode satisfies \(f'(x) = 0\) M1
\(f'(x) = \frac{{{\lambda ^{n + 1}}}}{{n!}}\left( {n{x^{n – 1}}{{\text{e}}^{ – \lambda x}} – \lambda {x^n}{{\text{e}}^{ – \lambda x}}} \right)\) A1
mode \( = \frac{n}{\lambda }\) A1
[6 marks]
(c) (i) \({\text{P}}(T > t) = {\text{P}}(0,{\text{ }}1{\text{ or 2 arrivals in }}[0,{\text{ }}t])\) (M1)
\( = {{\text{e}}^{ – 8t}} + {{\text{e}}^{ – 8t}} \times 8t + {{\text{e}}^{ – 8t}} \times \frac{{{{(8t)}^2}}}{2}\) A1
\( = {{\text{e}}^{ – 8t}}\left( {1 + 8t + 32{t^2}} \right)\) AG
(ii) differentiating,
\( – f(t) = – 8{{\text{e}}^{ – 8t}}\left( {1 + 8t + 32{t^2}} \right) + {{\text{e}}^{ – 8t}}(8 + 64t)\) A1A1
Note: Award A1 for LHS, A1 for RHS.
\(f(t) = 256{t^2}{{\text{e}}^{ – 8t}}\) A1
(iii) with the previous notation, \(n = 2,{\text{ }}\lambda = 8\). (M1)
mean \( = \frac{3}{8}\) A1
mode \( = \frac{1}{4}\) A1
[8 marks]
Note: Do not follow through if they use a negative probability density function.
[27 marks]
Question
The random variable \(X\) has probability density function given by
\[f(x) = \left\{ {\begin{array}{*{20}{l}}
{x{{\text{e}}^{ – x}},}&{{\text{for }}x \geqslant 0,} \\
{0,}&{{\text{otherwise}}}
\end{array}} \right..\]
A sample of size 50 is taken from the distribution of \(X\).
a.Use l’Hôpital’s rule to show that \(\mathop {\lim }\limits_{x \to \infty } \frac{{{x^3}}}{{{{\text{e}}^x}}} = 0\).[3]
b.(i) Find \({\text{E}}({X^2})\).
(ii) Show that \({\text{Var}}(X) = 2\).[10]
c.State the central limit theorem.[2]
d.Find the probability that the sample mean is less than 2.3.[2]
▶️Answer/Explanation
Markscheme
attempt to apply l’Hôpital’s rule M1
\(\mathop {\lim }\limits_{x \to \infty } \frac{{3{x^2}}}{{{{\text{e}}^x}}}\) A1
then \(\mathop {\lim }\limits_{x \to \infty } \frac{{6x}}{{{{\text{e}}^x}}}\)
then \(\mathop {\lim }\limits_{x \to \infty } \frac{6}{{{{\text{e}}^x}}}\) A1
\( = 0\) AG
[3 marks]
(i) \({\text{E}}({X^2}) = \mathop {\lim }\limits_{R \to \infty } \int\limits_0^R {{x^3}{{\text{e}}^{ – x}}{\text{d}}x} \) M1
attempt at integration by parts M1
the integral \( = [ – {x^3}{{\text{e}}^{ – x}}]_0^R + \mathop \smallint \limits_0^R 3{x^2}{{\text{e}}^{ – x}}{\text{d}}x\) A1A1
\( = [ – {x^3}{{\text{e}}^{ – x}}]_0^R + [ – 3{x^2}{{\text{e}}^{ – x}}]_0^R + \int\limits_0^R {6x{{\text{e}}^{ – x}}{\text{d}}x} \) M1
\( = [ – {x^3}{{\text{e}}^{ – x}}]_0^R + [ – 3{x^2}{{\text{e}}^{ – x}}]_0^R + [ – 6x{{\text{e}}^{ – x}}]_0^R + \int\limits_0^R {6{{\text{e}}^{ – x}}{\text{d}}x} \) A1
\( = [ – {x^3}{{\text{e}}^{ – x}}]_0^R + [ – 3{x^2}{{\text{e}}^{ – x}}]_0^R + [ – 6x{{\text{e}}^{ – x}}]_0^R + [ – 6{{\text{e}}^{ – x}}]_0^R\) A1
\( = 6\) when \(R \to \infty \) R1
(ii) \({\text{E}}(X) = 2\) A1
\({\text{Var}}(X) = {\text{E}}({X^2}) – {\left( {{\text{E}}(X)} \right)^2} = 6 – {2^2}\) M1
\( = 2\) AG
[10 marks]
if a random sample of size \(n\) is taken from any distribution \(X\), with \({\text{E}}(X) = \mu \) and \({\text{Var}}(X) = {\sigma ^2}\), then, for large n, A1
the sample mean \(\bar X\) has approximate distribution \({\text{N}}\left( {\mu ,{\text{ }}\frac{{{\sigma ^2}}}{n}} \right)\) A1
[2 marks]
\(\bar X \sim {\text{N}}\left( {2,{\text{ }}\frac{2}{{50}} = {{(0.2)}^2}} \right)\) (A1)
\({\text{P}}(\bar X < 2.3) = \left( {{\text{P}}(Z < 1.5)} \right) = 0.933\) A1
[2 marks]
