Question
The following diagram shows the weighted graph G .
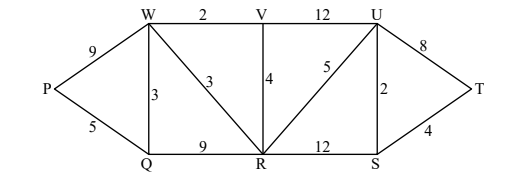
Write down a Hamiltonian circuit in G starting at P. [1]
(i) State what feature of G enables you to deduce that it is not bipartite.(ii) Explain why G does not have an Eulerian trail.
(iii) An edge is removed from G , creating a new graph H , which does have an Eulerian trail. Identify all the possibilities for this edge. [5]
(i) Use Dijkstra’s algorithm in G to find the minimum weight path from P to T .
(ii) State the total weight of this path. [8]
▶️Answer/Explanation
Ans:
(a) PQRSTUVWP or PWVUTSRQP
(b)
(i) G is not bipartite because it contains triangles (odd cycles) Note: Accept an adjacency argument showing that a particular vertex (for example, W ) cannot belong to two disjoint vertex sets. The feature in this instance is the particular vertex.
(ii) G does not have an Eulerian trail because it has more than two vertices (four vertices, Q, V, R and S) of odd degree (iii) remove an edge joining two vertices of odd degree: Q, V , Rand S H would now have an Eulerian trail three possible edges are: QR or RS or RV
(c)
(i)
EITHER 
OR
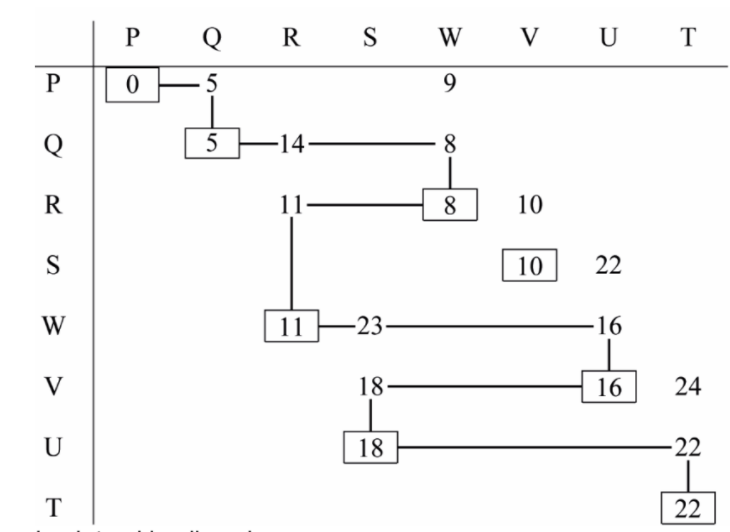
back tracking line shown THENthe minimum weight path is PQWRUST
(ii) with weight 22
Question
The following diagram shows a weighted graph \(G\) .
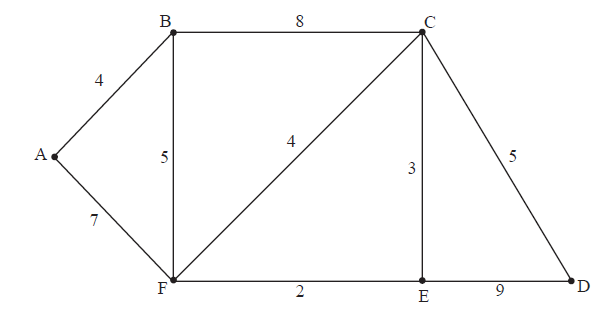
a.(i) Explain briefly what features of the graph enable you to state that \(G\) has an Eulerian trail but does not have an Eulerian circuit.
(ii) Write down an Eulerian trail in \(G\) .[3]
b.(i) Use Kruskal’s algorithm to find and draw the minimum spanning tree for \(G\) . Your solution should indicate the order in which the edges are added.
(ii) State the weight of the minimum spanning tree.[5]
c.Use Dijkstra’s algorithm to find the path of minimum total weight joining A to D, and state its weight. Your solution should indicate clearly the use of this algorithm.[10]
▶️Answer/Explanation
Markscheme
(i) \(G\) has an Eulerian trail because it has \(2\) vertices of odd degree and the remaining vertices of even degree R1
\(G\) does not have an Eulerian circuit because not all vertices are of even degree R1
(ii) BAFBCFECDE A1
[3 marks]
(i) the edges are added in the order
FE A1
CE
AB A1
BF, CD
or CD, BF A1
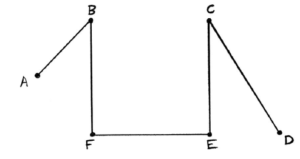
A1
(ii) minimum weight is \(19\) A1
[5 marks]

the shortest path is AFCD A2
the weight is \(16\) A1
[10 marks]
Examiners report
This question was attempted by the majority of students with at least partial success by most. Most candidates were able to give a partial explanation of the condition for a graph to have an Eulerian trail and not an Eulerian circuit, but few were able to provide the required detail. Most candidates were able to write down an Eulerian trail in \(G\). Many candidates successfully applied Kruskal’s algorithm and Dijkstra’s algorithm, but a number of candidates did not appreciate the significance of the order of adding edges in Kruskal’s algorithm, and the explanations of Dijkstra’s algorithm were sometimes poor.
This question was attempted by the majority of students with at least partial success by most. Most candidates were able to give a partial explanation of the condition for a graph to have an Eulerian trail and not an Eulerian circuit, but few were able to provide the required detail. Most candidates were able to write down an Eulerian trail in G. Many candidates successfully applied Kruskal’s algorithm and Dijkstra’s algorithm, but a number of candidates did not appreciate the significance of the order of adding edges in Kruskal’s algorithm, and the explanations of Dijkstra’s algorithm were sometimes poor.
This question was attempted by the majority of students with at least partial success by most. Most candidates were able to give a partial explanation of the condition for a graph to have an Eulerian trail and not an Eulerian circuit, but few were able to provide the required detail. Most candidates were able to write down an Eulerian trail in \(G\). Many candidates successfully applied Kruskal’s algorithm and Dijkstra’s algorithm, but a number of candidates did not appreciate the significance of the order of adding edges in Kruskal’s algorithm, and the explanations of Dijkstra’s algorithm were sometimes poor.
Question
Use the Euclidean algorithm to show that the greatest common divisor of 411 and 339 is 3.
▶️Answer/Explanation
Ans
411= 1 × 339 + 72
339 = 4 × 72 + 51
72 = 1 × 51 + 21
51= 2 × 21 +9
21= 2 × 9 +2
(9 = 3 × 3 + 0 )
the GCD is 3
Question
The following diagram shows a weighted graph G with vertices A, B, C, D and E.
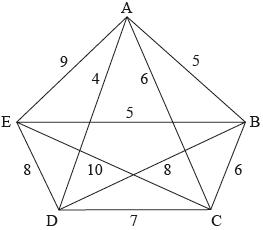
a.Show that graph \(G\) is Hamiltonian. Find the total number of Hamiltonian cycles in \(G\), giving reasons for your answer.[3]
b.State an upper bound for the travelling salesman problem for graph \(G\).[1]
d.Hence find a lower bound for the travelling salesman problem for \(G\)[2]
e.Show that the lower bound found in (d) cannot be the length of an optimal solution for the travelling salesman problem for the graph \(G\).[3]
▶️Answer/Explanation
Markscheme
eg the cycle \({\text{A}} \to {\text{B}} \to {\text{C}} \to {\text{D}} \to {\text{E}} \to {\text{A}}\) is Hamiltonian A1
starting from any vertex there are four choices
from the next vertex there are three choices, etc … R1
so the number of Hamiltonian cycles is \(4!{\text{ }}( = 24)\) A1
Note: Allow 12 distinct cycles (direction not considered) or 60 (if different starting points count as distinct). In any case, just award the second A1 if R1 is awarded.
[3 marks]
total weight of any Hamiltonian cycles stated
eg \({\text{A}} \to {\text{B}} \to {\text{C}} \to {\text{D}} \to {\text{E}} \to {\text{A}}\) has weight \(5 + 6 + 7 + 8 + 9 = 35\) A1
[1 mark]
a lower bound for the travelling salesman problem is then obtained by adding the weights of CA and CB to the weight of the minimum spanning tree (M1)
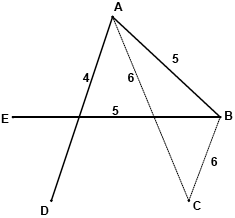
a lower bound is then \(14 + 6 + 6 = 26\) A1
[2 marks]
METHOD 1
eg eliminating A from G, a minimum spanning tree of weight 18 is (M1)
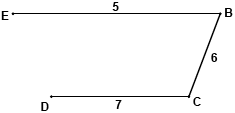
A1
adding AD and AB to the spanning tree gives a lower bound of \(18 + 4 + 5 = 27 > 26\) A1
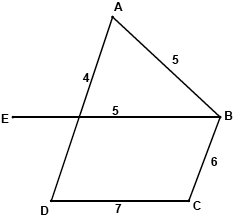
so 26 is not the best lower bound AG
Note: Candidates may delete other vertices and the lower bounds obtained are B-28, D-27 and E-28.
METHOD 2
there are 12 distinct cycles (ignoring direction) with the following lengths
Cycle Length
ABCDEA 35 M1
ABCEDA 33
ABDCEA 39
ABDECA 37
ABECDA 31
ABEDCA 31
ACBDEA 37
ACBEDA 29
ACDBEA 35
ACEBDA 33
AEBCDA 31
AECBDA 37 A1
as the optimal solution has length 29 A1
26 is not the best possible lower bound AG
Note: Allow answers where candidates list the 24 cycles obtained by allowing both directions.
[3 marks]
Examiners report
Part (a) was generally well answered, with a variety of interpretations accepted.
Part (b) also had a number of acceptable possibilities.
Part (d) was generally well answered, but there were few good attempts at part (e).
Part (d) was generally well answered, but there were few good attempts at part (e).
Question
A canal system divides a city into six land masses connected by fifteen bridges, as shown in the diagram below.
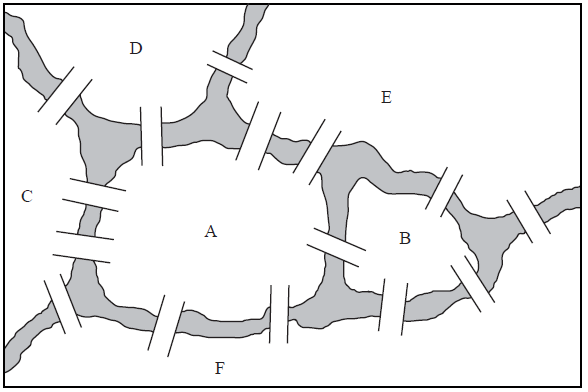
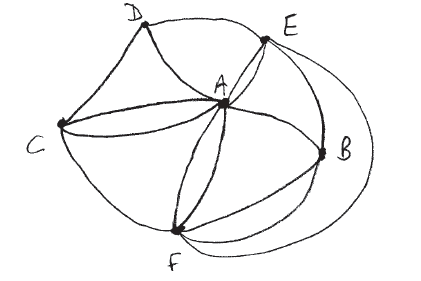
a.Draw a planar graph to represent this map.[2]
b.Write down the adjacency matrix of the graph.[2]
c.List the degrees of each of the vertices.[2]
d.State with reasons whether or not this graph has
(i) an Eulerian circuit;
(ii) an Eulerian trail.[4]
e.Find the number of walks of length \(4\) from E to F.[2]
▶️Answer/Explanation
Markscheme
 A2
A2
[2 marks]
A2
Note: Award A1 for one error or omission, A0 for more than one error or omission. Two symmetrical errors count as one error.
[2 marks]
A B C D E F
(8, 4, 4, 3, 5, 6) A2
[2 marks]
(i) no, because there are odd vertices M1A1
(ii) yes, because there are exactly two odd vertices M1A1
[4 marks]
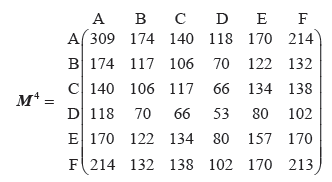
number of walks of length \(4\) is \(170\) (M1)A1
Note: The complete matrix need not be shown. Only one of the FE has to be shown.
[2 marks]
Question
A.a.The graph \(H\) has the following adjacency matrix.

(i) Show that \(H\) is bipartite.
(ii) Draw \(H\) as a planar graph.[3]
A.b.(i) Explain what feature of \(H\) guarantees that it has an Eulerian circuit.
(ii) Write down an Eulerian circuit in \(H\) .[3]
A.c.(i) Find the number of different walks of length five joining A to B.
(ii) Determine how many of these walks go through vertex F after passing along two edges.[6]
A.d.Find the maximum number of extra edges that can be added to \(H\) while keeping it simple, planar and bipartite.[4]
B.a.Find the smallest positive integer \(m\) such that \({3^m} \equiv 1(\bmod 22)\) .[2]
B.b.Given that \({3^{49}} \equiv n(\bmod 22)\) where \(0 \le n \le 21\) , find the value of \(n\) .[4]
B.c.Solve the equation \({3^x} \equiv 5(\bmod 22)\) .[3]
▶️Answer/Explanation
Markscheme
(i) using any method, (M1)
find that \(\left\{ {{\rm{A,C,D,F}}} \right\}\) and \(\left\{ {{\rm{B,E,G}}} \right\}\) are disjoint sets of vertices A1
so that \(H\) is bipartite AG
(ii)
A1
[3 marks]
(i) all vertices are of even degree A1
(ii) DECBAGFBD A2
[3 marks]
(i)
M1
number of walks \( = 36\) A1
(ii) recognition of the need to find walks of length \(2\) and walks of length \(3\) (M1)
number of walks of length \(2\) from A to F \( = 2\) A1
number of walks of length \(3\) from F to B \( = 6\) A1
required number of walks \( =12\) A1
[6 marks]
for a simple, bipartite graph to be planar,
\(e \le 2v – 4 = 10\) M1
at the moment, \(e = 8\) which means that we cannot add more than \(2\) edges A1
we see that we can add \(2\) edges, e.g. EA and EF A1
the maximum number of edges we can add is therefore \(2\) A1
[4 marks]
evaluating successive powers of \(3\) (M1)
\({3^1} \equiv 3(\bmod 22)\) , \({3^2} \equiv 9(\bmod 22)\) , \({3^3} \equiv 5(\bmod 22)\)
\({3^4} \equiv 15(\bmod 22)\) , \({3^5} \equiv 1(\bmod 22)\) so \(m = 5\) A1
[2 marks]
since \({3^5} \equiv 1(\bmod 22)\) , \({3^{45}} = {({3^5})^9} \equiv 1(\bmod 22)\) M1A1
consider \({3^{49}} = {3^{45}} \times {3^4} \equiv 1 \times 15(\bmod 22)\) so \(n = 15\) M1A1
[4 marks]
from (a), \(x = 3\) is a solution A1
since \({3^5} \equiv 1(\bmod 22)\) , the complete solution is \(x = 3 + 5N\) where \(N \in \bullet \) (M1)A1
[3 marks]
