IB Mathematics SL 3.1 The distance between two points AA SL Paper 2- Exam Style Questions- New Syllabus
Question
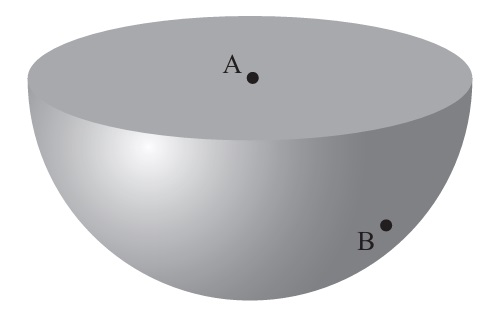
The diagram shows a solid hemisphere with centre \( A(6,-1,-3) \). Point \( B(4,-5,-9) \) lies on the curved surface.
(a) Find \( AB \), the radius of the hemisphere.
(b) Hence, find the total surface area of the solid hemisphere.
(b) Hence, find the total surface area of the solid hemisphere.
Most-appropriate topic codes (IB Mathematics AA SL 2025):
• SL 3.1: Distance between two points in 3D — part (a)
• SL 3.1: Surface area of 3D solids (hemisphere) — part (b)
• SL 3.1: Surface area of 3D solids (hemisphere) — part (b)
▶️ Answer/Explanation
(a)
Using the 3D distance formula:
\( AB = \sqrt{(6-4)^2 + (-1+5)^2 + (-3+9)^2} \)
\( = \sqrt{2^2 + 4^2 + 6^2} = \sqrt{4 + 16 + 36} = \sqrt{56} \)
\( AB = 2\sqrt{14} \) (exact) or \( \approx 7.48 \) (to 3 s.f.).
(b)
Total surface area of a solid hemisphere:
Curved surface area \( = 2\pi r^2 \), base area \( = \pi r^2 \)
Total \( = 3\pi r^2 \).
Using \( r = 2\sqrt{14} \):
\( r^2 = 56 \)
\( \text{Surface area} = 3\pi \times 56 = 168\pi \) (exact) \( \approx 528 \) (to 3 s.f.).