Question
The angle θ satisfies the equation tanθ + cotθ = 3. Find all the possible values of θ in \([0^o, 90^o]\).
▶️Answer/Explanation
Ans
METHOD 1
\(tanθ + \frac{1}{tanθ}=3 \Rightarrow tan^2θ-3 tanθ + 1 = 0\)
\(tanθ=\frac{3\pm\sqrt{5}}{2}\)
=0.382, 2.618
θ = 20.9o, 69.1o
METHOD 2
\(\frac{sinθ}{sinθ}+\frac{cosθ}{sinθ}=3\Rightarrow \frac{1}{sinθcosθ}=3\)
\(\Rightarrow \frac{1}{sin 2θ}=\frac{3}{2}\)
\(\Rightarrow sin 2θ=\frac{2}{3}\)
\(\Rightarrow θ=20.9^o, 69.1^o\)
Question
(a) Sketch the graph of y = cos(4x), in the interval 0≤x≤\(\pi\),
(b) On the same diagram sketch the graph of y=sec(4x), for 0≤x≤\(\pi\),
by indicating clearly the equations of any asymptotes.
(c) Use your sketch to solve
(i) the equation sec(4x)=-1, for 0≤x≤\(\pi\).
(ii) the inequality cos(4x)≤0, for 0≤x≤\(\pi\).
▶️Answer/Explanation
Ans
(a) and (b)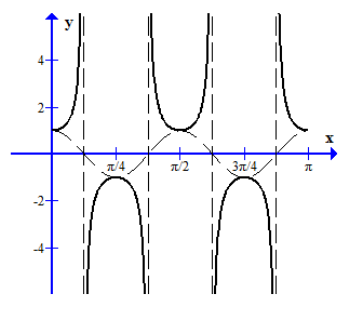
(c) (i) \(x=\frac{\pi}{4}, x=\frac{3\pi}{4}\) (ii) \(\frac{\pi}{8}≤x≤\frac{3\pi}{8}\) or \(\frac{5\pi}{8}≤x≤\frac{7\pi}{8}\).
Question
The diagram below shows the boundary of the cross-section of a water channel.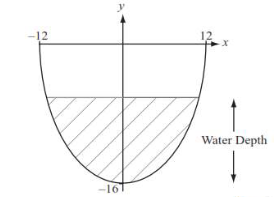
The equation that represents this boundary is y=16sec(\(\frac{\pi x}{36}\))-32 where x and y are both measured in cm.
The top of the channel is level with the ground and has a width of 24cm. The maximum depth of the channel is 16 cm.
Find the width of the water surface in the channel when the water depth is 10 cm. Give your answer in the form a arccosb where a,b ∈\(\mathbb{R}\).
▶️Answer/Explanation
Ans
10 cm water depth corresponds to 16sec(\(\frac{\pi x}{36}\)0=k or equivalent i.e. making a trigonometrical function the subject of the equation.
\(cos(\frac{\pi x}{36})=\frac{8}{13}\)
\(\frac{\pi x}{36}=\pm arccos\frac{8}{13}\)
Width of water surface is \(\frac{72}{\pi}\) arccos \(\frac{8}{13}\) (cm)
Question
Let f be the function f(x) = x arccos x + \(\frac{1}{2}x\) for -1≤x≤1 and g the funtion g(x) = cos 2x for -1≤x≤1.
(a) On the grid below, sketch the graph of f and of g.
(b) Write down the solution of the equation f(x) = g(x). _______
(c) Write down the range of g. _______________
▶️Answer/Explanation
Ans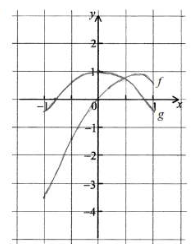
(b) x = 0.412
(c) Accept [-0.416,1] or [-0.416,1] or [cos2,1],[cos(-2),1].
Question
(a) Show that \(\arctan \left( {\frac{1}{2}} \right) + \arctan \left( {\frac{1}{3}} \right) = \frac{\pi }{4}\) .
(b) Hence, or otherwise, find the value of \(\arctan (2) + \arctan (3)\) .
▶️Answer/Explanation
Markscheme
(a) METHOD 1
let \(x = \arctan \frac{1}{2} \Rightarrow \tan x = \frac{1}{2}\) and \(y = \arctan \frac{1}{3} \Rightarrow \tan y = \frac{1}{3}\)
\(\tan (x + y) = \frac{{\tan x + \tan y}}{{1 – \tan x\tan y}} = \frac{{\frac{1}{2} + \frac{1}{3}}}{{1 – \frac{1}{2} \times \frac{1}{3}}} = 1\) M1
so, \(x + y = \arctan 1 = \frac{\pi }{4}\) A1AG
METHOD 2
for \(x,{\text{ }}y > 0\) , \(\arctan x + \arctan y = \arctan \left( {\frac{{x + y}}{{1 – xy}}} \right)\) if \(xy < 1\) M1
so, \(\arctan \frac{1}{2} + \arctan \frac{1}{3} = \arctan \left( {\frac{{\frac{1}{2} + \frac{1}{3}}}{{1 – \frac{1}{2} \times \frac{1}{3}}}} \right) = \frac{\pi }{4}\) A1AG
METHOD 3
an appropriate sketch M1
e.g. 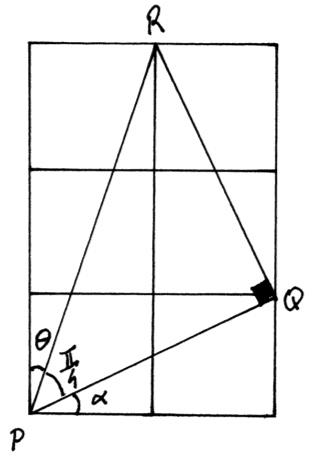
correct reasoning leading to \(\frac{\pi }{4}\) R1AG
(b) METHOD 1
\(\arctan (2) + \arctan (3) = \frac{\pi }{2} – \arctan \left( {\frac{1}{2}} \right) + \frac{\pi }{2} – \arctan \left( {\frac{1}{3}} \right)\) (M1)
\( = \pi – \left( {\arctan \left( {\frac{1}{2}} \right) + \arctan \left( {\frac{1}{3}} \right)} \right)\) (A1)
Note: Only one of the previous two marks may be implied.
\( = \pi – \frac{\pi }{4} = \frac{{3\pi }}{4}\) A1 N1
METHOD 2
let \(x = \arctan 2 \Rightarrow \tan x = 2\) and \(y = \arctan 3 \Rightarrow \tan y = 3\)
\(\tan (x + y) = \frac{{\tan x + \tan y}}{{1 – \tan x\tan y}} = \frac{{2 + 3}}{{1 – 2 \times 3}} = – 1\) (M1)
as \(\frac{\pi }{4} < x < \frac{\pi }{2}\,\,\,\,\,\left( {{\text{accept }}0 < x < \frac{\pi }{2}} \right)\)
and \(\frac{\pi }{4} < y < \frac{\pi }{2}\,\,\,\,\,\left( {{\text{accept }}0 < y < \frac{\pi }{2}} \right)\)
\(\frac{\pi }{2} < x + y < \pi \,\,\,\,\,{\text{(accept }}0 < x + y < \pi )\) (R1)
Note: Only one of the previous two marks may be implied.
so, \(x + y = \frac{{3\pi }}{4}\) A1 N1
METHOD 3
for \(x,{\text{ }}y > 0\) , \(\arctan x + \arctan y = \arctan \left( {\frac{{x + y}}{{1 – xy}}} \right) + \pi {\text{ if }}xy > 1\) (M1)
so, \(\arctan 2 + \arctan 3 = \arctan \left( {\frac{{2 + 3}}{{1 – 2 \times 3}}} \right) + \pi \) (A1)
Note: Only one of the previous two marks may be implied.
\( = \frac{{3\pi }}{4}\) A1 N1
METHOD 4
an appropriate sketch M1
e.g. 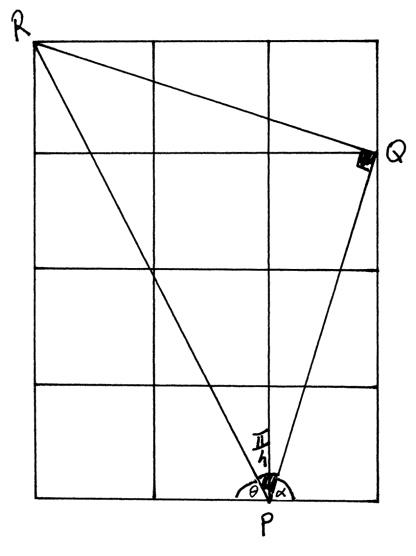
correct reasoning leading to \(\frac{{3\pi }}{4}\) R1A1
[5 marks]
Question
(a) Write down the domain and the range of the function f(x) = arctan x.
(b) By applying tan, find the values of
\(A=arctan\frac{1}{3}+arctan\frac{1}{2},\) \(B=arctan 2 + arctan 3\)
\(C=arctan\frac{1}{3}-arctan2\) \(D=arctan\frac{2}{3}+arctan\frac{3}{2}\)
▶️Answer/Explanation
Ans
(a) x∈R, \(-\frac{\pi}{2}<y<\frac{\pi}{2}\)
(b) \(tan A = 1 \Rightarrow A=\frac{\pi}{4}\) \(tan B=-1 \Rightarrow B=\frac{3\pi}{4}\) (B is +tive)
\(tan C=-1\Rightarrow C=-\frac{\pi}{4}\), (C is -tive) tan D not defined \(\Rightarrow D=\frac{\pi}{2}\)Questions 23-25 : without GDC.
Question
Solve \(tan^22θ=1\), in the interval \(-\frac{\pi}{2}≤θ≤\frac{\pi}{2}\)
▶️Answer/Explanation
Ans
\(tan^22\theta = 1\)
\(\Rightarrow tan 2\theta=\pm 1\)
\(\theta = \pm \frac{3\pi}{4},\pm \frac{\pi}{4}\)
\(\Rightarrow = \pm\frac{3\pi}{8},\pm\frac{\pi}{8}\) or \(\pm 1.18, \pm 0.393\)
