Question
[Maximum mark: 5]
Let \(f(x)=\frac{3x^{2}}{5x-1}\).
(a) Write down the equation of the vertical asymptote of \(y = f (x)\) .
(b) Find \({f}'(x)\) . Give your answer in the form \(\frac{ax^{2}+bx}{(5x-1)^{2}}\) where \(a\) and \(b\in \mathbb{Z}\) .
▶️Answer/Explanation
Ans.
(a)\(x=\frac{1}{5}\)
(b)\({f}'(x)=\frac{(5x-1)(6x)-(3x^{2})(5)}{(5x-1)^{2}}=\frac{30x^{2}-6x-15x^{2}}{(5x-1)^{2}}=\frac{15x^{2}-6x}{(5x-1)^{2}}\)
Question
[Maximum mark: 6]
The following diagram shows an isosceles triangle ABC with AB = 10 cm and AC = BC. The
vertex C is moving in a direction perpendicular to (AB) with speed 2 cm per second.
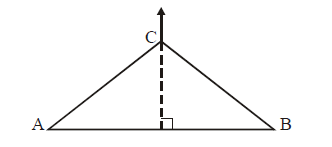
Calculate the rate of increase of the angle CAB at the moment the triangle is equilateral.
▶️Answer/Explanation
Ans.
Let h = height of triangle and θ = \(\hat{CAB}\).
\(h=5tan\Theta \Rightarrow \frac{dh}{dt}=\frac{5}{cos^{2}x}\frac{d\Theta }{dt}\)
Put \(\Theta =\frac{\pi }{3}\). 2=5x4x\(\frac{d\Theta }{dt}\)
\(\frac{d\Theta }{dt}=\frac{1}{10}\) rad per sec ( Accept\(\frac{18^{\circ}}{\pi }\) per second or \(5.73^{\circ}\)per second )
Question
[Maximum mark: 6]
An airplane is flying at a constant speed at a constant altitude of 3 km in a straight line
that will take it directly over an observer at ground level. At a given instant the observer
notes that the angle θ is \(\frac{1}{3}\)π radians and is increasing at \(\frac{1}{60}\) radians per second.
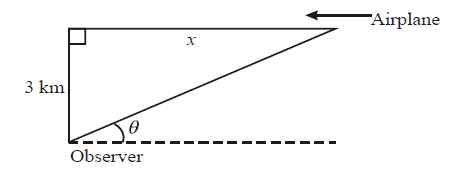
Find the speed, in kilometres per hour, at which the airplane is moving towards the observer.
▶️Answer/Explanation
Ans.
\(tan\;\Theta =\frac{3}{x}\Rightarrow \frac{1}{cos^{2}\Theta }\frac{d\Theta }{dt}=\frac{-3}{x^{2}}\frac{dx}{dt}\)
When \(\Theta =\frac{\pi }{3},x^{2}=3\) and \(cos^{2}\Theta =\frac{1}{4}\)
Hence, \(4\frac{1}{60}=-\frac{dx}{dt}\Rightarrow \frac{dx}{dt}=-\frac{1}{15}km\;s^{-1}=-240\;km\;h^{-1}\)
The aeroplane is moving towards him at 240 km \(h^{-1}\)
Question
[Maximum mark: 5]
In the previous problem, find the rate of change of the distance between the observer
and the airplane, at the instant when the angle θ is \(\frac{1}{3}\)π radians and is increasing at \(\frac{1}{60}\) radians per second.
▶️Answer/Explanation
Ans.
If \(z\) is the distance then \(z^{2}=3^{2}+x^{2}\Rightarrow z^{2}=9+x^{2}\)
Then \(2z\frac{dz}{dt}=2x\frac{dx}{dt}\Rightarrow z\frac{dz}{dt}=x\frac{dx}{dt}\)
When \(\Theta =\frac{\pi }{3}, x=\sqrt{3},z\sqrt{12}=2\sqrt{3}\) and \(\frac{dx}{dt}\)=-240 km \(h^{-1}\)
Hence,
\(\Rightarrow 2\sqrt{3}\frac{dz}{dt}=-240\sqrt{3}\Rightarrow \frac{dz}{dt}\)=-240 km \(h^{-1}\)
Question
[Maximum mark: 6]
A conical tank with vertex down is 8 metres in diamater and 12 meters deep. Water
flows into the tank at 10 m3 per minute. Find the rate of change of the depth of the
water at the instant when the water is 6 meters deep.
▶️Answer/Explanation
Ans.
\(\frac{r}{h}=\frac{4}{12}\Rightarrow r=\frac{h}{3}\)
\(V=\frac{\pi }{3}\left (\frac{h}{3} \right )^{2}(h)\)
\(V=\frac{\pi }{27}h^{3}\)
\(\frac{dV}{dt}=\frac{\pi }{9}h^{2}\frac{dh}{dt}\)
\(10=\frac{\pi }{9}(6)^{2}\frac{dh}{dt}\)
\(\frac{dh}{dt}=\frac{90}{36\pi }\left ( =\frac{5}{2\pi }=0.796 \right )\) metres per min
Question
[Maximum mark: 5]
In problem 9, answer the same question if Car A was travelling in an easternly direction.
▶️/Explanation
Ans.
Then \(\frac{dx}{dt}=60\) (positive) , \(\frac{dz}{dt}\) =+0.8 x 60 – 0.6 x 70 = 6 km h-1
